Государственное бюджетное общеобразовательное учреждение

Самарской области средняя общеобразовательная

школа № 2 им. В. Маскина ж.-д. ст. Клявлино

муниципального района Клявлинский

Самарской области

« Уравнения

и

неравенства

с параметрами»

учебное пособие

Клявлино

Учебное пособие

« Уравнения и неравенства с параметрами» для учащихся 10 –11 классов

данное пособие является приложением к программе элективного курса «Уравнения и неравенства с параметрами», которая прошла внешнюю экспертизу (научно-методическим экспертным советом министерства образования и науки Самарской области от 19 декабря 2008 года бала рекомендована к использованию в образовательных учреждениях Самарской области)

Авторы

Ромаданова Ирина Владимировна

учитель математики МОУ Клявлинской средней общеобразовательной

школы № 2 им. В.Маскина Клявлинского района Самарской области

Сербаева Ирина Алексеевна

Введение……………………………………………………………3-4

Линейные уравнения и неравенства с параметрами……………..4-7

Квадратные уравнения и неравенства с параметрами……………7-9

Дробно- рациональные уравнения с параметрами……………..10-11

Иррациональные уравнения и неравенства с параметрами……11-13

Тригонометрические уравнения и неравенства с параметрами.14-15

Показательные уравнения и неравенства с параметрами………16-17

Логарифмические уравнения и неравенства с параметрами…...16-18

Задачи ЕГЭ………………………………………………………...18-20

Задания для самостоятельной работы…………………………...21-28

Введение.

Уравнения и неравенства с параметрами.

Если в уравнении или неравенстве некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а само уравнение или неравенство параметрическим.

Для того, чтобы решить уравнение или неравенство с параметрами необходимо:

Выделить особое значение - это то значение параметра, в котором или при переходе через которое меняется решение уравнения или неравенства.

Определить допустимые значения – это значения параметра, при которых уравнение или неравенство имеет смысл.

Решить уравнение или неравенство с параметрами означает:

1) определить, при каких значениях параметров существуют решения;

2) для каждой допустимой системы значений параметров найти соответствующее множество решений.

Решить уравнение с параметром можно следующими методами: аналитическим или графическим.

Аналитический метод предполагает задачу исследования уравнения рассмотрением нескольких случаев, ни один из которых нельзя упустить.

Решение уравнения и неравенства с параметрами каждого вида аналитическим методом предполагает подробный анализ ситуации и последовательное исследование, в ходе которого возникает необходимость «аккуратного обращения» с параметром.

Графический метод предполагает построение графика уравнения, по которому можно определить, как влияет соответственно, на решение уравнения изменение параметра. График подчас позволяет аналитически сформулировать необходимые и достаточные условия для решения поставленной задач. Графический метод решения особенно эффективен тогда, когда нужно установить, сколько корней имеет уравнение в зависимости от параметра и обладает несомненным преимуществом увидеть это наглядно.

§ 1. Линейные уравнения и неравенства.

Линейное уравнение а x = b , записанное в общем виде, можно рассматривать как уравнение с параметрами, где x – неизвестное, a , b – параметры. Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном.

При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.

Особым значением параметра a является значение а = 0.

b = 0 является особым значением параметра b .

При b ¹ 0 уравнение решений не имеет.

При b = 0 уравнение примет вид: 0х = 0 . Решением данного уравнения является любое действительное число.

Неравенства вида ах > b и ax < b (а ≠ 0) называются линейными неравенствами. Множество решений неравенства ах > b – промежуток

(; +), если a > 0 , и (-;) , если а < 0 . Аналогично для неравенства

ах < b множество решений – промежуток (-;), если a > 0, и (; +), если а < 0.

Пример 1. Решить уравнение ах = 5

Решение : Это линейное уравнение.

Если а = 0 , то уравнение 0 × х = 5 решения не имеет.

Если а ¹ 0, х = - решение уравнения.

Ответ : при а ¹ 0, х=

при а = 0 решения нет.

Пример 2. Решить уравнение ах – 6 = 2а – 3х.

Решение: Это линейное уравнение, ах – 6 = 2а – 3х (1)

ах + 3х = 2а +6

Переписав уравнение в виде (а+3)х = 2(а+3) , рассмотрим два случая:

а= -3 и а ¹ -3.

Если а= -3 , то любое действительное число х является корнем уравнения (1). Если же а ¹ -3 , уравнение (1) имеет единственный корень х = 2.

Ответ: При а = -3, х R ; при а ¹ -3, х = 2.

Пример 3. При каких значениях параметра а среди корней уравнения

2ах – 4х – а 2 + 4а – 4 = 0 есть корни больше 1 ?

Решение : Решим уравнение 2ах – 4х – а 2 + 4а – 4 = 0 – линейное уравнение

2(а - 2) х = а 2 – 4а +4

2(а - 2) х = (а – 2) 2

При а = 2 решением уравнения 0х = 0 будет любое число, в том числе и большее 1.

При а ¹ 2 х =
. По условию х > 1 , то есть
>1, а > 4.

Ответ: При а {2} U (4;∞).

Пример 4 . Для каждого значения параметра а найти количество корней уравнения ах=8.

Решение. ах = 8 – линейное уравнение.

y = a – семейство горизонтальных прямых;

y = - графиком является гипербола. Построим графики этих функций.

Ответ: Если а =0 , то уравнение решений не имеет. Если а ≠ 0 , то уравнение имеет одно решение.

Пример 5 . С помощью графиков выяснить, сколько корней имеет уравнение:

|х| = ах – 1.

y =| х | ,

y = ах – 1 – графиком является прямая, проходящая через точку (0;-1).

Построим графики этих функций.

Ответ:При|а|>1 - один корень

при | а| ≤1 – уравнение корней не имеет.

Пример 6 . Решить неравенство ах + 4 > 2х + а 2

Решение : ах + 4 > 2х + а 2
(а – 2) х > а 2 – 4. Рассмотрим три случая.

Ответ. х > а + 2 при а > 2; х <а + 2, при а < 2; при а=2 решений нет.

§ 2. Квадратные уравнения и неравенства

Квадратное уравнение – это уравнение вида ах ² + b х + с = 0 , где а≠ 0,

а, b , с – параметры.

Для решения квадратных уравнений с параметром можно использовать стандартные способы решения на применение следующих формул:

1 ) дискриминанта квадратного уравнения: D = b ² - 4 ac , (
²- ас)

2) формул корней квадратного уравнения: х 1 =
, х 2 =
,

(х 1,2 =
)

Квадратными называются неравенства вида

a х 2 + b х + с > 0, a х 2 + b х + с< 0, (1), (2)

a х 2 + b х + с ≥ 0, a х 2 + b х + с ≤ 0, (3), (4)

Множество решений неравенства (3) получается объединением множеств решений неравенства (1) и уравнения , a х 2 + b х + с=0. Аналогично находится множество решений неравенства (4).

Если дискриминант квадратного трехчлена a х 2 + b х + с меньше нуля, то при а >0 трехчлен положителен при всех х R .

Если квадратный трехчлен имеет корни (х 1 < х 2 ), то при а > 0 он положителен на множестве (-; х 2 )
(х 2; +) и отрицателен на интервале

(х 1 ; х 2 ). Если а < 0, то трехчлен положителен на интервале (х 1 ; х 2 ) и отрицателен при всех х (-; х 1 )
(х 2; +).

Пример 1. Решить уравнение ах² - 2 (а – 1)х – 4 = 0 .

Это квадратное уравнение

Решение : Особое значение а = 0.

При а = 0 получим линейное уравнение 2х – 4 = 0 . Оно имеет единственный корень х = 2.

При а ≠ 0. Найдем дискриминант.

D = (а-1)² + 4а = (а+1)²

Если а = -1, то D = 0 – один корень.

Найдем корень, подставив вместо а = -1.

-х² + 4х – 4= 0, то есть х² -4х + 4 = 0, находим, что х=2.

Если а ≠ - 1 , то D >0 . По формуле корней получим: х=
;

х 1 =2, х 2 = -.

Ответ: При а=0 и а= -1 уравнение имеет один корень х = 2; при а ≠ 0 и

а ≠ - 1 уравнение имеет два корня х 1 =2, х 2 =-.

Пример 2. Найдите количество корней данного уравнения х²-2х-8-а=0 в зависимости от значений параметра а.

Решение. Перепишем данное уравнение в виде х²-2х-8=а

y = х²-2х-8 - графиком является парабола;

y =а - семейство горизонтальных прямых.

Построим графики функций.

Ответ: При а <-9 , уравнение решений не имеет; при а=-9, уравнение имеет одно решение; при а>-9 , уравнение имеет два решения.

Пример 3. При каких а неравенство (а – 3) х 2 – 2ах + 3а – 6 >0 выполняется для всех значений х?

Решение. Квадратный трехчлен положителен при всех значениях х, если

а-3 > 0 и D <0, т.е. при а, удовлетворяющих системе неравенств

, откуда следует, что a > 6 .

Ответ. a > 6

§ 3. Дробно- рациональные уравнения с параметром,

сводящиеся к линейным

Процесс решения дробных уравнений выполняется по обычной схеме: дробное заменяется целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. После чего решается целое уравнение, исключая посторонние корни, то есть числа, которые обращают знаменатель в нуль.

В случае уравнений с параметром эта задача более сложная. Здесь, чтобы «исключить» посторонние корни, требуется найти значение параметра, обращающее общий знаменатель в нуль, то есть решить соответствующие уравнения относительно параметра.

Пример 1. Решить уравнение
= 0

Решение: Д.З: х +2 ≠ 0 , х ≠ -2

х – а = 0, х = а.

Ответ: При а ≠ - 2, х=а

При а = -2 корней нет.

Пример 2 . Решить уравнение
-
=
(1)

Это дробно- рациональное уравнение

Решение: Значение а = 0 является особым. При а = 0 уравнение теряет смысл и, следовательно, не имеет корней. Если а ≠ 0, то после преобразований уравнение примет вид: х² + 2 (1-а) х + а² - 2а – 3 = 0 (2) – квадратное уравнение.

Найдем дискриминант = (1 – а)² - (а² - 2а – 3)= 4, находим корни уравнения х 1 = а + 1, х 2 = а - 3.

При переходе от уравнения (1) к уравнению (2) расширилась область определения уравнения (1), что могло привести к появлению посторонних корней. Поэтому, необходима проверка.

П р о в е р к а. Исключим из найденных значений х такие, при которых

х 1 +1=0, х 1 +2=0, х 2 +1=0, х 2 +2=0.

Если х 1 +1=0, то есть (а+1) + 1= 0 , то а= -2. Таким образом,

при а= -2 , х 1 -

Если х 1 +2=0, то есть (а+1)+2=0, то а = - 3 . Таким образом, при а = - 3, х 1 - посторонний корень уравнения. (1).

Если х 2 +1=0, то есть (а – 3) + 1= 0 , то а = 2 . Таким образом, при а = 2 х 2 - посторонний корень уравнения (1).

Если х 2 +2=0, то есть (а – 3) + 2 = 0, то а=1 . Таким образом, при а = 1,

х 2 - посторонний корень уравнения (1).

В соответствии с этим при а = - 3 получаем х = - 3 – 3 = -6 ;

при а = - 2 х = -2 – 3= - 5;

при а = 1 х =1 + 1= 2;

при а = 2 х=2+1 = 3.

Можно записать ответ.

Ответ: 1) если а= -3, то х= -6; 2) если а= -2 , то х= -5 ; 3) если а= 0 , то корней нет; 4) если а= 1 , то х= 2; 5) если а=2 , то х=3 ; 6) если а ≠ -3, а ≠ -2, а ≠ 0, а≠ 1, а ≠ 2, то х 1 = а + 1, х 2 = а-3.

§4. Иррациональные уравнения и неравенства

Уравнения и неравенства, в которых переменная содержится под знаком корня, называется иррациональным.

Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной. При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение, учитывая при этом изменения значений параметра.

Уравнение вида
=g (x ) равносильно системе

Неравенство f (x ) ≥ 0 следует из уравнения f (x ) = g 2 (x ).

При решении иррациональных неравенств будем использовать следующие равносильные преобразования:

≤ g(x)


≥g(x)

Пример 1. Решите уравнение
= х + 1 (3)

Это иррациональное уравнение

Решение: По определению арифметического корня уравнение (3) равносильно системе
.

При а = 2 первое уравнение системы имеет вид 0 х = 5 , то есть не имеет решений.

При а≠ 2 х=
. Выясним, при каких значениях а найденное значение х удовлетворяет неравенству х ≥ -1:
≥ - 1,
≥ 0,

откуда а ≤ или а > 2.

Ответ: При а≤, а > 2 х=
, при < а ≤ 2 уравнение решений не имеет.

Пример 2. Решить уравнение
= а (приложение 4)

Решение. y =

y = а – семейство горизонтальных прямых.

Построим графики функций.

Ответ : при а<0 –решений нет;

при а ≥ 0 – одно решение.

Пример 3 . Решим неравенство (а+1)
<1.

Решение. О.Д.З. х ≤ 2 . Если а+1 ≤0 , то неравенство выполняется при всех допустимых значениях х . Если же а+1>0 , то

(а+1)
<1.

<

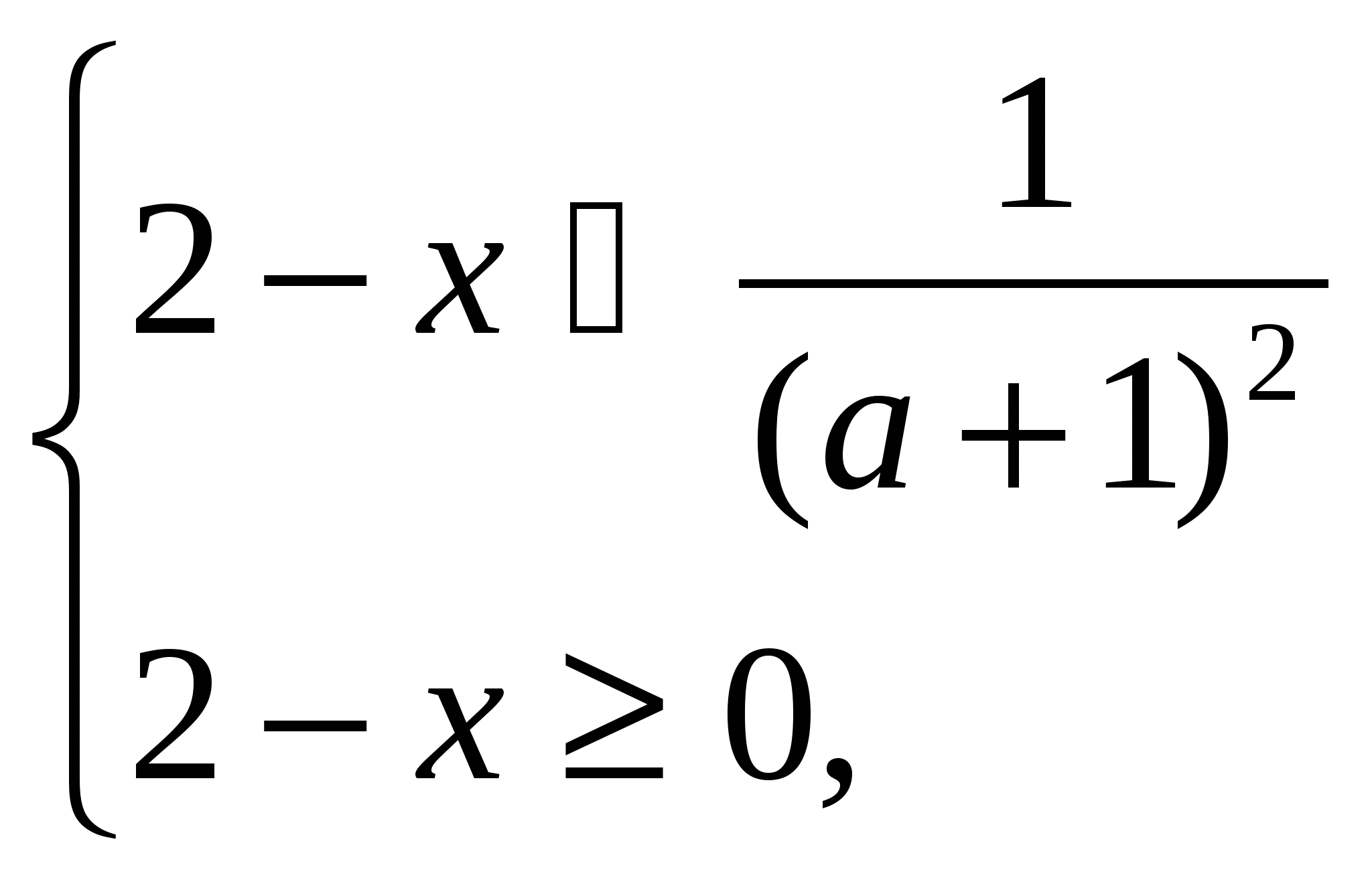
откуда х (2-
2

Ответ. х (- ;2 при а (-;-1, х (2-
2

при а (-1;+).

§ 5. Тригонометрические уравнения и неравенства.

Приведем формулы решений простейших тригонометрических уравнений:

Sinx = a
x= (-1) n arcsin a+πn, n Z, ≤1, (1)

Cos x = a
x = ±arccos a + 2 πn, n Z, ≤1. (2)

Если >1, то уравнения (1) и (2) решений не имеют.

tg x = a
x= arctg a + πn, n Z, aR

ctg x = a
x = arcctg a + πn, n Z, aR

Для каждого стандартного неравенства укажем множество решений:

1. sin x > a
arcsin a + 2 πn Z,

при a <-1, xR ; при a ≥ 1, решений нет.

2. . sin x < a
π - arcsin a + 2 πnZ,

при а≤-1, решений нет; при а >1, xR

3. cos x > a
- arccos a + 2 πn < x < arccos a + 2 πn , n Z ,

при а<-1, xR ; при a ≥ 1 , решений нет.

4. cos x arccos a+ 2 πnZ,

при а≤-1 , решений нет; при a > 1, x R

5. tg x > a, arctg a + πnZ

6. tg x < a, -π/2 + πn Z

Пример1. Найти а , при которых данное уравнение имеет решение:

Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

Решение. Запишем уравнение в виде

с os 2 x + (2 a -4) cosx +(a – 5)(а+1) =0, решая его как квадратное, получаем cosx = 5-а и cosx = -а-1.

Уравнение cosx = 5- а имеет решения при условии -1≤ 5- а ≤1
4≤ а ≤ 6, а уравнение cosx = - а-1 при условии -1≤ -1- а ≤ 1
-2 ≤ а ≤0.

Ответ. а -2; 0
4; 6

Пример 2. При каких b найдется а такое, что неравенство
+ b > 0 выполняется при всех х ≠ πn , n Z .

Решение. Положим а = 0. Неравенство выполняется при b >0. Покажем теперь, что ни одно b ≤0 не удовлетворяет условиям задачи. Действительно, достаточно положить х = π /2, если а <0, и х = - π /2 при а ≥0.

Ответ. b> 0

§ 6. Показательные уравнения и неравенства

1. Уравнение h (x ) f ( x ) = h (x ) g ( x ) при h (x ) > 0 равносильно совокупности двух систем
и

2. В частном случае (h (x )= a ) уравнение а f (x ) = а g (x ) при а > 0, равносильно совокупности двух систем

и

3. Уравнение а f (x ) = b , где а > 0, a ≠1, b >0, равносильно уравнению

f (x )= log a b . Случай а =1 рассматриваем отдельно.

Решение простейших показательных неравенств основано на свойстве степени. Неравенство вида f (a x ) > 0 при помощи замены переменной t = a x сводится к решению системы неравенств
а затем к решению соответствующих простейших показательных неравенств.

При решении нестрого неравенства необходимо к множеству решений строгого неравенства присоединить корни соответствующего уравнения. Как и при решении уравнений во всех примерах, содержащих выражение а f (x ) , предполагаем а > 0. Случай а = 1 рассматриваем отдельно.

Пример 1 . При каких а уравнение 8 х =
имеет только положительные корни?

Решение. По свойству показательной функции с основанием, большим единицы, имеем х>0
8 х >1

>1

>0, откуда a (1,5;4).

Ответ. a (1,5;4).

Пример 2. Решить неравенство a 2 ∙2 x > a

Решение . Рассмотрим три случая:

1. а< 0 . Так как левая часть неравенства положительна, а правая отрицательна, то неравенство выполняется для любых хR .

2. a =0. Решений нет.

3. а > 0 . a 2 ∙2 x > a
2 x >
x > - log 2 a

Ответ. хR при а > 0; решений нет при a =0; х (- log 2 a ; +) при а> 0 .

§ 7. Логарифмические уравнения и неравенства

Приведем некоторые эквивалентности, используемые при решении логарифмических уравнений и неравенств.

1. Уравнение log f (x ) g (x ) = log f (x ) h (x ) равносильно системе

В частности, если а >0, а ≠1, то

log a g (x)= log a h(x)

2. Уравнение log a g (x)=b
g (x)= a b ( а >0, a ≠ 1, g(x) >0).

3. Неравенство log f ( x ) g (x ) ≤ log f ( x ) h (x ) равносильно совокупности двух систем:
и

Если а, b – числа, а >0, а ≠1, то

log a f (x) ≤ b

log a f (x) > b

Пример 1. Решите уравнение

Решение . Найдем ОДЗ: х > 0, х ≠ а 4 , a > 0, а ≠ 1. Преобразуем уравнение

logх – 2 = 4 – log a x
logх + log a x – 6 = 0, откуда log a x = - 3

х = а -3 и log a x = 2
х = а 2 . Условие х = а 4
а – 3 = а 4 или а 2 = а 4 не выполняется на ОДЗ.

Ответ: х = а -3 , х = а 2 при а (0; 1)
(1; ).

Пример 2 . Найдите наибольшее значение а , при котором уравнение

2 log -
+ a = 0 имеет решения.

Решение. Выполним замену
= t и получим квадратное уравнение 2 t 2 – t + a = 0. Решая, найдем D = 1-8 a . Рассмотрим D ≥0, 1-8 а ≥0
а ≤.

При а = квадратное уравнение имеет корень t = >0.

Ответ. а =

Пример 3 . Решить неравенство log (x 2 – 2 x + a ) > - 3

Решение. Решим систему неравенств

Корни квадратных трехчленов х 1,2 = 1 ±
и х 3,4 = 1 ±
.

Критические значения параметра: а = 1 и а = 9.

Пусть Х 1 и Х 2 – множества решений первого и второго неравенств, тогда

Х 1
Х 2 = Х – решение исходного неравенства.

При 0< a <1 Х 1 = (- ;1 -
)
(1 +
; +), при а > 1 Х 1 = (-;+).

При 0 < a < 9 Х 2 = (1 -
; 1 +
), при а ≥9 Х 2 – решений нет.

Рассмотрим три случая:

1. 0< a ≤1 Х = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < a < 9 Х = (1 -
;1 +
).

3. a ≥ 9 Х – решений нет.

Задачи ЕГЭ

Высокий уровень С1, С2

Пример 1. Найдите все значения р , при которых уравнение

р ∙ ctg 2 x + 2sinx + p = 3 имеет хотя бы один корень.

Решение. Преобразуем уравнение

р ∙ (
- 1) + 2sinx + p = 3, sinx =t , t
, t 0.

- p + 2 t + p = 3, + 2 t = 3, 3 -2t = , 3t 2 – 2t 3 = p .

Пусть f (y ) = 3 t 2 – 2 t 3 . Найдем множество значений функции f (x ) на


. у / = 6 t – 6 t 2 , 6 t - 6 t 2 = 0, t 1 =0, t 2 = 1. f (-1) = 5, f (1) = 1.

При t
, E (f ) =
,

При t
, E (f ) =
, то есть при t


, E (f ) =
.

Чтобы уравнение 3 t 2 – 2 t 3 = p (следовательно, и данное) имело хотя бы один корень необходимо и достаточно p E (f ), то есть p
.

Ответ.
.

Пример 2.

При каких значениях параметра а уравнение log
(4 x 2 – 4 a + a 2 +7) = 2 имеет ровно один корень?

Решение. Преобразуем уравнение в равносильное данному:

4x 2 – 4a + a 2 +7 = (х 2 + 2) 2 .

Отметим, что если некоторое число х является корнем полученного уравнения, то число – х также является корнем этого уравнения. По условию это не выполнимо, поэтому единственным корнем является число 0.

Найдем а .

4∙ 0 2 - 4a + a 2 +7 = (0 2 + 2) 2 ,

a 2 - 4a +7 = 4, a 2 - 4a +3 = 0, a 1 = 1, a 2 = 3.

Проверка.

1) a 1 = 1. Тогда уравнение имеет вид: log
(4 x 2 +4) =2. Решаем его

4x 2 + 4 = (х 2 + 2) 2 , 4x 2 + 4 = х 4 + 4x 2 + 4, х 4 = 0, х = 0 – единственный корень.

2) a 2 = 3. Уравнение имеет вид: log
(4 x 2 +4) =2
х = 0 – единственный корень.

Ответ. 1; 3

Высокий уровень С4, С5

Пример 3. Найдите все значения р, при которых уравнение

х 2 – (р + 3)х + 1= 0 имеет целые корни и эти корни являются решениями неравенства: х 3 – 7р х 2 + 2х 2 – 14 р х - 3х +21 р ≤ 0.

Решение. Пусть х 1, х 2 – целые корни уравнения х 2 – (р + 3)х + 1= 0. Тогда по формуле Виета справедливы равенства х 1 + х 2 = р + 3, х 1 ∙ х 2 = 1. Произведение двух целых чисел х 1 , х 2 может равняться единице только в двух случаях: х 1 = х 2 = 1 или х 1 = х 2 = - 1. Если х 1 = х 2 = 1, то р + 3 = 1+1 = 2
р = - 1; если х 1 = х 2 = - 1, то р + 3 = - 1 – 1 = - 2
р = - 5. Проверим являются ли корни уравнения х 2 – (р + 3)х + 1= 0 в описанных случаях решениями данного неравенства. Для случая р = - 1, х 1 = х 2 = 1 имеем

1 3 – 7 ∙ (- 1) ∙ 1 2 +2∙ 1 2 – 14 ∙ (- 1) ∙ 1 – 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 – верно; для случая р = - 5, х 1 = х 2 = - 1 имеем (- 1) 3 – 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 – 14 ∙ (-5) × (- 1) – 3 ∙ (- 1) + 21∙ (-5) = - 136 ≤ 0 – верно. Итак, условию задачи удовлетворяют только р = - 1 и р = - 5.

Ответ. р 1 = - 1 и р 2 = - 5.

Пример 4. Найдите все положительные значения параметра а , при которых число 1 принадлежит области определения функции

у = (а
- а
).

Предварительный просмотр:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ

ГОУ НПО профессиональное училище № 37

ПРОЕКТ:

КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ С ПАРАМЕТРАМИ»

Выполнила –

Мацук Галина Николаевна,

Преподаватель математики ГОУ НПО

профессионального училища № 37 МО.

Г.Ногинск, 2011

1. Введение

4. Методика решения квадратных уравнений при начальных условиях.

6. Методика решения квадратных неравенств с параметрами в общем виде.

7. Методика решения квадратных неравенств при начальных условиях.

8.Заключение.

9.Литература.

1. Введение.

Основная задача обучения математике в профессиональном училище заключается в обеспечении прочного и сознательного овладения обучающимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности, достаточных для изучения смежных дисциплин и продолжения образования, а также в профессиональной деятельности, требующей достаточной высокой математической культуры.

Профилированное обучение математике осуществляется через решение задач прикладного характера, связанных с профессиями по металлообработке, электромонтажным работам, деревообработке. Для жизни в современном обществе важным является формирование математического стиля общения, проявляющегося в определенных умственных навыках. Задачи с параметрами обладают диагностической и прогностической ценностью. С их помощью можно проверить знания основных разделов элементарной математики, уровень логического мышления, первоначальные навыки исследовательской работы.

Обучение задачам с параметрами требует от обучающихся больших умственных и волевых усилий, развитого внимания, воспитания таких качеств, как активность, творческая инициатива, коллективно-познавательный труд. Задачи с параметрами ориентированы для изучения во время обобщающего повторения на 2 курсе в период подготовки к итоговой государственной аттестации и на 3 курсе на дополнительных занятиях при подготовке обучающихся, изъявивших желание сдавать выпускные экзамены в форме ЕГЭ.

Основным направлением модернизации математического образования является отработка механизмов итоговой аттестации через введение ЕГЭ. В заданиях по математике в последние годы вводятся задачи с параметрами. Обязательны такие задания на вступительных экзаменах в вузы. Появление таких задач очень актуально, так как с их помощью проверяется техника владения формулами элементарной математики, методами решения уравнений и неравенств, умение выстраивать логическую цепочку рассуждений, уровень логического мышления абитуриента. Анализ предыдущих результатов ЕГЭ за несколько предыдущих лет показывает, что выпускники с большим трудом решают такие задания, а многие даже не приступают к ним. Большинство либо вовсе не справляются с такими заданиями, либо приводят громоздкие выкладки. Причиной этого является отсутствие системы заданий по данной теме в школьных учебниках. В связи с этим возникла необходимость в проведении в выпускных группах при подготовке к экзаменам специальных тем по решению задач с параметрами и задач прикладного характера, связанных с профессиональной направленностью.

Изучение данных тем предназначено для обучающихся 3 курса, которые хотят научиться способам решения задач повышенного уровня сложности по алгебре и началам анализа. Решение таких задач вызывает у них значительные затруднения. Это связано с тем, что каждое уравнение или неравенство с параметрами представляет собой целый класс обычных уравнений и неравенств, для каждого из которых должно быть получено решение.

В процессе решения задач с параметрами в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ, классификация и систематизация, аналогия. Так как в учебном плане в профессиональных училищах предусмотрено проведение консультаций по математике, которые имеются в расписании учебных занятий, то для обучающихся, обладающих достаточной математической подготовкой, проявляющих интерес к изучаемому предмету, имеющих дальнейшей целью поступление в вуз, целесообразно использовать указанные часы для решения задач с параметрами для подготовки к олимпиадам, математическим конкурсам, различного рода экзаменам, в частности ЕГЭ. Особенно актуально решение таких задач для прикладного и практического характера, которое поможет при проведении различных исследований.

2. Цели, основные задачи, методы, технологии, требования к знаниям.

Цели проекта:

• Формирование умений и навыков по решению задач с параметрами, сводящихся к исследованию квадратных уравнений и неравенств.
• Формирование интереса к предмету, развитие математических способностей, подготовка к ЕГЭ.
• Расширение математических представлений о приемах и методах решения уравнений и неравенств.
• Развитие логического мышления и навыков исследовательской деятельности.
• Приобщение к творческой, исследовательской и познавательной деятельности.
• Обеспечение условий для самостоятельной творческой работы.
• Воспитание у обучающихся умственных и волевых усилий, развитого внимания, активности, творческой инициативы, умений коллективно-познавательного труда.

Основные задачи проекта:

• Предоставить обучающимся возможность реализовать свой интерес к математике и индивидуальные возможности для его освоения.
• Способствовать усвоению фактических знаний и умений.
• Показать практическую значимость задач с параметрами в сфере прикладного исследования.
• Научить способам решения стандартных и нестандартных уравнений и неравенств.
• Углубить знания по математике, предусматривающие формирование устойчивого интереса к предмету.
• Выявить и развить математические способности обучающихся.
• Обеспечить подготовку к поступлению в вузы.
• Обеспечить подготовку к профессиональной деятельности, требующей высокой математической культуры.
• Организовать исследовательскую и проектную деятельность, способствующую развитию интеллектуальных и коммуникативных качеств.

Методы, используемые при проведении занятий:

• Лекция – для передачи теоретического материала, сопровождающаяся беседой с обучающимися.
• Семинары – для закрепления материла по обсуждению теории.
• Практикумы – для решения математических задач.
• Дискуссии – для аргументации вариантов своих решений.
• Различные формы групповой и индивидуальной деятельности.
• Исследовательская деятельность, которая организуется через: работу с дидактическим материалом, подготовку сообщений, защиту рефератов и творческих работ.
• Лекции – презентации с использованием компьютера и проектора.

Используемые технологии:

• Лекционно-семинарская система обучения.
• Информационно-коммуникационные технологии.
• Исследовательский метод в обучении, направленный на развитие мыслительных способностей.
• Проблемное обучение, предусматривающую мотивацию к исследованию путем постановки проблемы, обсуждение различных вариантов проблемы.
• Технология деятельностного метода, помогающая вывить познавательные интересы обучающихся.

Требования к знаниям обучающихся.

В результате изучения различных способов решения квадратных уравнений и неравенств с параметрами обучающиеся должны приобрести умения:

• Прочно усвоить понятие параметра в квадратном уравнении и квадратном неравенстве;
• Уметь решать квадратные уравнения с параметрами.
• Уметь решать квадратные неравенства с параметрами.
• Находить корни квадратичной функции.
• Строить графики квадратичных функций.
• Исследовать квадратичный трехчлен.
• Применять рациональные приемы тождественных преобразований.
• Использовать наиболее употребляемые эвристические приемы.
• Уметь применять полученные знания при работе на персональном компьютере.

Формы контроля.

• Уроки – самооценки и оценки товарищей.
• Презентация учебных проектов.
• Тестирование.
• Рейтинг – таблица.
• Домашние задачи из сборников по ЕГЭ прошлых лет.
• Контрольные работы.

3. Методика решения квадратных уравнений с параметрами в общем виде.

Не надо бояться задач с параметрами. Прежде всего при решении уравнений и неравенств с параметрами надо сделать то, что делается при решении любого уравнения и неравенства – привести заданные уравнения или неравенства к более простому виду, если это возможно: разложить рациональное выражение на множители, сократить, вынести множитель за скобки и т.д. Встречаются задачи, которые можно разделить на два больших класса.

В первый класс можно отнести примеры, в которых надо решить уравнение или неравенство при всех возможных значениях параметра.

Ко второму классу отнесем примеры, в которых надо найти не все возможные решения, а лишь те из них, которые удовлетворяют некоторым дополнительным условиям. Класс таких задач неисчерпаем.

Наиболее понятный для обучающихся способ решения таких задач состоит в том, что сначала находят все решения, а затем отбирают те, которые удовлетворяют дополнительным условиям.

При решении задач с параметрами иногда удобно строить графики в обычной плоскости (х,у), а иногда лучше рассмотреть графики в плоскости (х,а), где х – независимая переменная, а «а» – параметр. Это прежде всего возможно в задаче, где приходится строить знакомые элементарные графики: прямые, параболы, окружности и т.д. Кроме того эскизы графиков иногда помогают наглядно увидеть и «ход» решения.

При решении уравнений f (х,а) = 0 и неравенств f (х,а) › 0 надо помнить, что в первую очередь рассматривают решение при тех значениях параметра, при которых обращается в ноль коэффициент при старшей степени х квадратного трехчлена f (х,а), понижая тем самым степень. Квадратное уравнение А(а) х 2 + В(а) х + С(а) = 0 при А(а) = 0 превращается в линейное, если при этом В(а) ≠ 0, а методы решения квадратных и линейных уравнений различны.

Вспомним основные формулы для работы с квадратными уравнениями.

Уравнение вида ах 2 + вх + с = 0, где х  R – неизвестные, а, в, с – выражения, зависящие только от параметров, причем а ≠ 0, называется квадратным уравнением, а D = b 2 – 4ас называется дискриминантом квадратного трехчлена.

Если D

Если D > 0, то уравнение имеет два различных корня

х 1 = , х 2 = , и тогда ах 2 + вх + с = а (х – х 1 ) (х – х 2 ).

Эти корни через коэффициенты уравнения связаны формулами Виета

Если D = 0, то уравнение имеет два совпадающих корня х 1 = х 2 = , и тогда ах 2 + вх + с = а (х – х 1 ) 2 . В этом случае говорят, что уравнение имеет одно решение.

Когда , т.е. = 2к, корни квадратного уравнения определяются по формуле х 1,2 = ,

Для решения приведенного квадратного уравнения х 2 + pх + q = 0

Используется формула х 1,2 = - , а также формулы Виета

Примеры. Решить уравнения:

Пример 1. + =

Решение:

При а ≠ - 1, х ≠ 2 получаем х 2 + 2ах – 3в + 4 = 0 и корни

х 1 = - а - , х 2 = -а + , существующие при

А 2 + 2а – 4  0, т.е. при

Теперь проверим, нет ли таких а, при которых либо х 1 , либо х 2 равен 2. Подставим в квадратное уравнение х = 2, при этом получим а = - 8.

Второй корень в таком случае равен (по теореме Виета) и при а = - 8 равен 14.

Ответ: при а = - 8 единственное решение х = 14;

Если а  (- ∞; - 8)  (- 8; - 4)  (1; + ∞) – два корня х 1 и х 2 ;

Если а = - единственное решение х = соответственно;

Если а  (- 4; 1), то х   .

Иногда уравнения с дробными членами приводятся к квадратным. Рассмотрим следующее уравнение.

Пример 2. - =

Решение: При а = 0 оно не имеет смысла, значение х должно удовлетворять условиям: х  -1, х  -2. Умножив все члены уравнения на а (х + 1) (х +2)  0,

Получим х 2 – 2(а – 1)х + а 2 – 2а – 3 = 0, равносильное данному. Его корни:

х 1 = а + 1, х 2 = - 3. Выделим из этих корней посторонние, т.е. те, которые равны – 1 и – 2:

Х 1 = а + 1 = - 1, а = - 2, но при а = - 2 х 2 = - 5;

Х 1 = а + 1 = - 2, а = - 3, но при а = - 3 х 2 = - 6;

Х 2 = а - 3 = - 1, а = 2, но при а = 2 х 1 = 3;

Х 2 = а - 3 = - 2, а = 1, но при а = 1 х 1 = 2.

Ответ: при а ≠ 0, а ≠  2, а ≠ - 3, а ≠ 1 х 1 = а + 1, х 2 = а – 3;

При а = - 2 х = - 5; при а = - 3 х = - 6.

4.Методика решения квадратных уравнений при начальных условиях.

Условия параметрических квадратных уравнений разнообразны. Например, нужно найти значение параметра при котором корни: положительны, отрицательны, имеют разные знаки, больше или меньше какого-либо числа и т.д. Для их решения следует использовать свойства корней квадратного уравнения ах 2 + вх + с = 0.

Если D > 0, а > 0, то уравнение имеет два действительных различных корня, знаки которых при с > 0 одинаковы и противоположны знаку коэффициента в, а при с

Если D = 0, а > 0, то уравнение имеет действительные и равные между собой корни, знак которого противоположен знаку коэффициента в.

Если D 0, то уравнение не имеет действительных корней.

Аналогично можно установить свойства корней квадратного уравнения и для а

1. Если в квадратном уравнении поменять местами коэффициенты а и с, то получим уравнение, корни которого обратны корням данного.
2. Если в квадратном уравнении поменять знак коэффициента в, то получим уравнение, корни которого противоположны корням данного.
3. Если в квадратном уравнении коэффициенты а и с имеют разные знаки, то оно имеет действительные корни.
4. Если а > 0 и D = 0, то левая часть квадратного уравнения – есть полный квадрат, и наоборот, если левая часть уравнения есть полный квадрат, то а > 0 и D = 0.
5. Если все коэффициенты уравнения рациональны и дискриминант выражает полный квадрат, то корни уравнения рациональны.
6. Если рассматривается расположение корней относительно нуля, то применяем теорему Виета.

Отбор корней квадратного трехчлена по условиям и расположение нулей квадратичной функции на числовой прямой.

Пусть f (х) = ах 2 + вх + с, а  0, корни х 1 ˂ х 2 ,  ˂  .

	Расположение корней на числовой прямой.	Необходимое и достаточное условие.
	х 1 , х 2 	а f ( ) > 0, D  0, х 0 
	х 1 , х 2 > 	а f ( ) > 0, D  0, х 0 > 
	х 1  2	а f ( )
	 1 ,х 2  .	а f ( ) > 0, D  0, а f ( ) > 0  0  .
	 1  2	а f ( ) > 0, а f ( )
	х 1  2 	а f ( )  ) > 0
	х 1   2	а f ( )  )

Пример 3. Установить, при каких значениях а уравнение

х 2 – 2 (а – 1) х + 2а + 1 = 0

• не имеет корней:

необходимое и достаточное условие D

D = (а – 1) 2 – 2а – 1 = а 2 – 4а

• имеет корни:

D  0, D = (а – 1) 2 – 2а – 1  0, а 

• имеет один корень:

• имеет два корня:

D > 0, т.е. а 

• имеет положительные корни:

2(а – 1) > 0   а  4

Если вопрос будет «имеет два положительных корня», то в системе следует заменить D > 0;

• имеет отрицательные корни:

2(а – 1)  

• имеет корни разного знака, т.е. один положительный, а другой отрицательный:

  а ;

Условие использовать не обязательно, достаточно х 1 х 2

• имеет один из корней, равный 0:

необходимое достаточное условие – равенство нулю свободного члена уравнения, т.е. 2а + 1 = 0, а = -1/2.

Знак второго корня определяется или подстановкой в исходное уравнение а = -1/2, или, проще, по теореме Виета х 1 + х 2 = 2 (а – 1), и после подстановки а = -1/2 получаем х 2 = - 3, т.е. при а = -1/2 два корня: х 1 = 0, х 2 = - 3.

Пример 4 . При каких значениях параметра а уравнение

(а – 2) х 2 – 4ах +3 -2а = 0 имеет единственное решение, удовлетворяющее неравенству х

Решение.

Дискриминант 2 – (а – 2)(3 – 2а)

4а 2 – 3а + 6 + 2а 2 – 4а = 6а 2 – 7а + 6

Так как 49 – 144 = - 95 и первый коэффициент 6 то 6а 2 – 7а + 6 при всех х  R.

Тогда х 1,2 = .

По условию задачи х 2, тогда получим неравенство

Имеем:

верно при всех а  R.

6а 2 – 7а + 6 6а 2 – 7а - 10 2

А 1,2 = 1/12 (7  17), а 1 = 2, а 2 = - 5/6.

Следовательно, -5/6

Ответ: -

5. Параметр как равноправная переменная.

Во всех разобранных задачах параметр рассматривался как фиксированное, но неизвестное число. Между тем с формальной точки зрения параметр – это переменная, причем «равноправная» с другими, присутствующими в примере. К примеру, при таком взгляде на параметр формы f (х; а) задают функции не с одной (как ранее), а с двумя переменными. Подобная интерпретация, естественно формирует еще один тип (а точнее метод решения, определяющий этот тип) задач с параметрами. Покажем аналитическое решение такого типа.

Пример 5. На плоскости ху укажите все точки, через которые не проходит ни одна из кривых семейства у = х 2 – 4рх + 2р 2 – 3, где р – параметр.

Решение: Если (х 0 ;у 0 ) – точка, через которую не проходит ни одна из кривых заданного семейства, то координаты этой точки не удовлетворяют исходному уравнению. Следовательно, задача свелась к тому, чтобы найти зависимость между х и у, при которой данное в условии уравнение не имело бы решений. Нужную зависимость несложно получить, сосредоточив внимание не на переменных х и у, а на параметре р. В этом случае возникает продуктивная идея: рассмотреть данное уравнение как квадратное относительно р. Имеем

2р 2 – 4рх+ х 2 – у – 3 = 0. Дискриминант = 8х 2 + 8у + 24 должен быть отрицательным. Отсюда получаем у ˂ - х 2 – 3, следовательно, искомое множество – это все точки координатной плоскости, лежащие «под» параболой у = - х 2 – 3.

Ответ : у 2 – 3

6. Методика решения квадратных неравенств с параметрами

В общем виде.

Квадратными (строгими и нестрогими) называются неравенства вида

Допустимыми являются те значения параметров, при которых а,в,с – действительны. Квадратные неравенства удобно решать либо аналитическим способом, либо графическим. Так как графиком квадратичной функции является парабола, то при а > 0 ветви параболы направлены вверх, при а

Различное положение параболы f (х) = ах 2 + вх + с, а  0 при а > 0 показано на рис.1

А) в) с)

а) Если f (х) > 0 и D  R;

б) Если f (х) > 0 и D = 0, то х  ;

в) Если f (х) > 0 и D > 0, то х  (-  ; х 1 )  (х 2 ; +  ).

Аналогично рассматриваются положения параболы при а

Например, один из трех случаев, когда

при а 0 и f (х) > 0 х  (х 1 ; х 2 );

при а 0 и f (х)  (-  ; х 1 )  (х 2 ; +  ).

В качестве примера рассмотрим решение неравенства.

Пример 6. Решить неравенство х 2 + 2х + а > 0.

Пусть D – дискриминант трехчлена х 2 + 2х + а > 0. При D = 0, при а = 1, неравенство примет вид:

(х + 1) 2 > 0

Оно верно при любых действительных значениях х, кроме х = - 1.

При D > 0, т.е. при х , трехчлен х 2 + 2х + а имеет два корня: - 1 – и

1 + и решением неравенства служит промежуток

(-  ; - 1 – )  (- 1 + ; +  )

Это неравенство легко решить графически. Для этого представим его в виде

Х 2 + 2х > - а

и построим график функции у = х 2 + 2х

Абсциссы точек пересечения этого графика с прямой у = - а и являются корнями уравнения х 2 + 2х = - а.

Ответ:

при –а > - 1, т.е. при а , х  (-  ; х 1 )  (х 2 ;+  );

при – а = - 1, т.е. при а = 1, х – любое действительное число, кроме - 1;

при – а , т.е при а > 1, х – любое действительное число.

Пример 7 . Решить неравенство сх 2 – 2 (с – 1)х + (с + 2)

При с = 0 оно принимает вид: 2х + 2 решением будет х

Введем обозначение f (х) = сх 2 – 2 (с – 1)х + (с + 2) где с ≠ 0.

В этом случае неравенство f (х)

Пусть и D – дискриминант f (х). 0,25 D = 1 – 4с.

Если D > 0, т.е. если с > 0,25, то знак f (х) совпадает со знаком с при любых действительных значениях х, т.е. f (х) > 0 при любых х  R, значит, при с > 0,25 неравенство f (х)

Если D = 0, т.е. с = 0,25, то f (х) = (0,25 х + 1,5) 2 , т.е. f (х)  0 при любом

Х  R. Следовательно, при с = 0,25 неравенство f (х)

Рассмотрим случай D  0). f (х) = 0 при двух действительных значениях х:

х 1 = (с – 1 – ) и х 2 = (с – 1 + ).

Здесь могут представиться два случая:

Решить неравенство f (х)

f (х) совпадает со знаком с. Чтобы ответить на этот вопрос, заметим, что – , т.е. с – 1 – ˂ с – 1 + ,но так как с (с – 1 – ) (с – 1 + ) и поэтому решением неравенства будет:

(-  ; (с – 1 – ))  ( (с – 1 + ); +  ).

Теперь для решения неравенства достаточно указать те значения с, при которых знак f (х) противоположен знаку с. Так как при 0 1 2 , то х  (х 1 ; х 2 ).

Ответ: при с = 0 х  R;

При с  (-  ; х 2 )  (х 1 ; +  );

При 0 (х 1 ; х 2 );

При с  0,25 решений нет.

Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах решения и квадратных неравенств. В самом деле, поскольку параметр «равен в правах» с переменной, то ему естественно, можно «выделить» и свою координатную ось. Таким образом возникает координатная плоскость (х; а). Такая незначительная деталь, как отказ от традиционного выбора букв х и у для обозначения осей, определяет один из самых эффективнейших методов решения задач с параметрами.

Удобно, когда в задаче фигурирует один параметр а и одна переменная х. Сам процесс решения схематично выглядит так. Вначале строится графический образ, затем, пересекая полученный график прямыми, перпендикулярными параметрической оси, «снимаем» нужную информацию.

Отказ от традиционного выбора букв х и у для обозначения осей, определяет один из эффективнейших методов решения задач с параметрами – «метод областей»

1. Методика решения квадратных неравенств при начальных условиях.

Рассмотрим аналитическое решение квадратного неравенства с параметрами, результаты решения которого рассматриваются на числовой прямой.

Пример 8.

Найдите все значения х, для каждого из которых неравенство

(2-х)а 2 +(х 2 -2х+3)а-3х≥0

выполняется для любого значения а, принадлежащего промежутку [-3;0].

Решение. Преобразуем левую часть данного неравенства следующим образом:

(2-x)а 2 + (x 2 -2x+3)а-3х=ах 2 - а 2 х - 2ах + 2а 2 + 3а - 3x =

Ах (х - а)-2а(х - а)- 3(х-а) = (x - а)(аx- 2а - 3).

Данное неравенство примет вид: (x - а) (аx - 2а - 3) ≥ 0.

Если а = 0, получаем - Зх ≥ 0 x ≤ 0.

Если а ≠ 0, то -3 а

Так как а 0, то решением этого неравенства будет промежуток числовой оси, расположенный между корнями соответствующего неравенству уравнения.

Выясним взаимное расположение чисел а и , учитывая при этом условие - 3 ≤ а

3 ≤a

A = -1.

Представим во всех рассмотренных случаях решения данного неравенства в зависимости от значений параметра:

Получим, что только х = -1 является решением данного неравенства при любом значении параметра а  .

Ответ: -1

8. Заключение.

Почему мной был выбран проект по теме «Разработка методических рекомендаций решения квадратных уравнений и неравенств с параметрами»? Так как при решении любых тригонометрических, показательных, логарифмических уравнений, неравенств, систем мы чаще всего приходим к рассмотрению иногда линейных, а чаще всего квадратных уравнений и неравенств. При решении сложнейших задач с параметрами большинство заданий сводится с помощью равносильных преобразований к выбору решений типа: а (х – а) (х – с) > 0 (

Мы рассмотрели теоретические основы для решения квадратных уравнений и неравенств с параметрами. Вспомнили необходимые формулы и преобразования, рассмотрели различные расположения графиков квадратичной функции в зависимости от значения дискриминанта, от знака при старшем коэффициенте, от расположения корней, вершины параболы. Выявили схему решения и выбора результатов, составили таблицу.

В проекте показаны аналитические и графические методы решения квадратных уравнений и неравенств. Обучающимся в профессиональном училище необходимо зрительное восприятие материала для лучшего усвоения материала. Показано, как можно поменять переменную х и принять параметр как равноправную величину.

Для наглядного усвоения данной темы рассмотрено решение 8 задач с параметрами, по 1 – 2 для каждого раздела. В примере № 1 рассмотрено количество решений при различных значениях параметра, в примере № 3 проводится разбор решения квадратного уравнения при самых различных начальных условиях. Для решения квадратных неравенств сделана графическая иллюстрация. В примере № 5 применяется метод замены параметра как равноправной величины. В проект включено рассмотрение примера № 8 из заданий, включенных в раздел С, для интенсивной подготовки к сдаче ЕГЭ.

Для качественной подготовки обучающихся решению задач с параметрами рекомендуется в полном объеме использовать мультимедийные технологии, а именно: использовать для лекций презентации, электронные учебники и книги, собственные разработки из медиатеки. Очень эффективны бинарные уроки математика + информатика. Незаменимым помощником преподавателю и учащемуся является Интернет. В презентации необходимы импортированные объекты из существующих образовательных ресурсов. Наиболее удобным и приемлемым в работе является ЦОР «Использование Microsoft Office в школе».

Разработка методических рекомендаций по данной тематике облегчит работу молодых преподавателей, пришедших работать в училище, пополнит портфолио преподавателя, послужит образцом для специальных предметов, образцы решений помогут обучающимся справиться со сложными заданиями.

9. Литература.

1.Горнштейн П.И., Полонский В.Б., ЯкирМ.С. Задачи с параметрами. «Илекса», «Гимназия», Москва – Харьков, 2002.

2.Балаян Э.Н. Сборник задач по математике для подготовки к ЕГЭ и олимпиадам. 9-11 классы. «Феникс», Ростов-на Дону, 2010.

3.Ястребинецкий Г.А. Задачи с параметрами. М., «Просвещение», 1986.

4.Колесникова С.И. Математика. Решение сложных задач Единого государственного экзамена. М. «АЙРИС – пресс», 2005.

5.Родионов Е.М., Синякова С.Л. Математика. Пособие для поступающих в вузы. Учебный центр «Ориентир» МГТУ им. Н.Э. Баумана, М., 2004.

6. Сканави М.И. Сборник задач по математике для поступающих в вузы: В 2 кн. Кн.1, М., 2009.

решение неравенства в режиме онлайн решение почти любого заданного неравенства онлайн . Математические неравенства онлайн для решения математики. Быстро найти решение неравенства в режиме онлайн . Сайт www.сайт позволяет найти решение почти любого заданного алгебраического , тригонометрического или трансцендентного неравенства онлайн . При изучении практически любого раздела математики на разных этапах приходится решать неравенства онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение неравенства онлайн займет несколько минут. Основное преимущество www.сайт при решении математических неравенства онлайн - это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические неравенства онлайн , тригонометрические неравенства онлайн , трансцендентные неравенства онлайн , а также неравенства с неизвестными параметрами в режиме онлайн . Неравенства служат мощным математическим аппаратом решения практических задач. C помощью математических неравенств можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины неравенств можно найти, сформулировав задачу на математическом языке в виде неравенств и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое неравенство , тригонометрическое неравенство или неравенства содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения неравенств . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических неравенств онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических неравенств онлайн , тригонометрических неравенств онлайн , а также трансцендентных неравенств онлайн или неравенств с неизвестными параметрами. Для практических задач по нахождению инетравол решений различных математических неравенств ресурса www.. Решая неравенства онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение неравенств на сайте www.сайт. Необходимо правильно записать неравенство и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением неравенства. Проверка ответа займет не более минуты, достаточно решить неравенство онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении неравенств онлайн будь то алгебраическое , тригонометрическое , трансцендентное или неравенство с неизвестными параметрами.

Изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Некоторые Вузы также включают в экзаменационные билеты уравнения, неравенства и их системы, которые часто бывают весьма сложными и требующими нестандартного подхода к решению. В школе же этот один из наиболее трудных разделов школьного курса математики рассматривается только на немногочисленных факультативных занятиях.

Готовя данную работу, я ставил цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. На мой взгляд графический метод является удобным и быстрым способом решения уравнений и неравенств с параметрами.

В моём реферате рассмотрены часто встречающиеся типы уравнений, неравенств и их систем, и, я надеюсь, что знания, полученные мной в процессе работы, помогут мне при сдаче школьных экзаменов и при поступлении а ВУЗ.

§ 1. Основные определения

Рассмотрим уравнение

¦(a, b, c, …, k, x)=j(a, b, c, …, k, x), (1)

где a, b, c, …, k, x -переменные величины.

Любая система значений переменных

а = а0, b = b0, c = c0, …, k = k0, x = x0,

при которой и левая и правая части этого уравнения принимают действительные значения, называется системой допустимых значений переменных a, b, c, …, k, x. Пусть А – множество всех допустимых значений а, B – множество всех допустимых значений b, и т.д., Х – множество всех допустимых значений х, т.е. аÎА, bÎB, …, xÎX. Если у каждого из множеств A, B, C, …, K выбрать и зафиксировать соответственно по одному значению a, b, c, …, k и подставить их в уравнение (1), то получим уравнение относительно x, т.е. уравнение с одним неизвестным.

Переменные a, b, c, …, k, которые при решении уравнения считаются постоянными, называются параметрами, а само уравнение называется уравнением, содержащим параметры.

Параметры обозначаются первыми буквами латинского алфавита: a, b, c, d, …, k, l, m, n а неизвестные – буквами x, y,z.

Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.

Два уравнения, содержащие одни и те же параметры, называются равносильными, если:

а) они имеют смысл при одних и тех же значениях параметров;

б) каждое решение первого уравнения является решением второго и наоборот.

§ 2. Алгоритм решения.

Находим область определения уравнения.

Выражаем a как функцию от х.

В системе координат хОа строим график функции а=¦(х) для тех значений х, которые входят в область определения данного уравнения.

Находим точки пересечения прямой а=с, где сÎ(-¥;+¥) с графиком функции а=¦(х).Если прямая а=с пересекает график а=¦(х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение а=¦(х) относительно х.

Записываем ответ.

I. Решить уравнение

(1)

Поскольку х=0 не является корнем уравнения, то можно разрешить уравнение относительно а:

или

График функции – две “склеенных” гиперболы. Количество решений исходного уравнения определяется количеством точек пересечения построенной линии и прямой у=а.

Если а Î (-¥;-1]È(1;+¥)È

, то прямая у=а пересекает график уравнения (1) в одной точке. Абсциссу этой точки найдем при решении уравнения относительно х.

Таким образом, на этом промежутке уравнение (1) имеет решение

. , то прямая у=а пересекает график уравнения (1) в двух точках. Абсциссы этих точек можно найти из уравнений и , получаем и . , то прямая у=а не пересекает график уравнения (1), следовательно решений нет.

Если а Î (-¥;-1]È(1;+¥)È

, то ; , то , ; , то решений нет.

II. Найти все значения параметра а, при которых уравнение

имеет три различных корня.

Переписав уравнение в виде

и рассмотрев пару функций , можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции , при которых он имеет точно три точки пересечения с графиком функции .

В системе координат хОу построим график функции

). Для этого можно представить её в виде и, рассмотрев четыре возникающих случая, запишем эту функцию в виде

Поскольку график функции

– это прямая, имеющая угол наклона к оси Ох, равный , и пересекающая ось Оу в точке с координатами (0 , а), заключаем, что три указанные точки пересечения можно получить лишь в случае, когда эта прямая касается графика функции . Поэтому находим производную .

III. Найти все значения параметра а, при каждом из которых система уравнений

имеет решения.

Из первого уравнения системы получим

при Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы “скользят” вершинами по оси абсцисс.

Выделим в левой части второго уравнения полные квадраты и разложим её на множители

Решение неравенств с параметром.

Неравенства, которые имеют вид ax > b, ax < b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются линейными неравенствами .

Принципы решения линейных неравенств с параметром очень схожи с принципами решения линейных уравнений с параметром.

Пример 1.

Решить неравенство 5х – а > ax + 3.

Решение.

Для начала преобразуем исходное неравенство:

5х – ах > a + 3, вынесем за скобки х в левой части неравенства:

(5 – а)х > a + 3. Теперь рассмотрим возможные случаи для параметра а:

Если a > 5, то x < (а + 3) / (5 – а).

Если а = 5, то решений нет.

Если а < 5, то x > (а + 3) / (5 – а).

Данное решение и будет являться ответом неравенства.

Пример 2.

Решить неравенство х(а – 2) / (а – 1) – 2а/3 ≤ 2х – а при а ≠ 1.

Решение.

Преобразуем исходное неравенство:

х(а – 2) / (а – 1) – 2х ≤ 2а/3 – а;

Ах/(а – 1) ≤ -а/3. Домножим на (-1) обе части неравенства, получим:

ах/(а – 1) ≥ а/3. Исследуем возможные случаи для параметра а:

1 случай. Пусть a/(а – 1) > 0 или а € (-∞; 0)ᴗ(1; +∞). Тогда x ≥ (а – 1)/3.

2 случай. Пусть a/(а – 1) = 0, т.е. а = 0. Тогда x – любое действительное число.

3 случай. Пусть a/(а – 1) < 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.

Ответ: х € [(а – 1)/3; +∞) при а € (-∞; 0)ᴗ(1; +∞);
х € [-∞; (а – 1)/3] при а € (0; 1);
х € R при а = 0.

Пример 3.

Решить неравенство |1 + x| ≤ аx относительно х.

Решение.

Из условия следует, что правая часть неравенства ах должна быть не отрицательна, т.е. ах ≥ 0. По правилу раскрытия модуля из неравенства |1 + x| ≤ аx имеем двойное неравенство

Ах ≤ 1 + x ≤ аx. Перепишем результат в виде системы:

{аx ≥ 1 + x;
{-ах ≤ 1 + x.

Преобразуем к виду:

{(а – 1)x ≥ 1;
{(а + 1)х ≥ -1.

Исследуем полученную систему на интервалах и в точках (рис. 1) :

При а ≤ -1 х € (-∞; 1/(а – 1)].

При -1 < а < 0 x € [-1/(а – 1); 1/(а – 1)].

При а = 0 x = -1.

При 0 < а ≤ 1 решений нет.

Графический метод решения неравенств

Построение графиков значительно упрощает решение уравнений, содержащих параметр. Использование графического метода при решении неравенств с параметром еще нагляднее и целесообразнее.

Графическое решение неравенств вида f(x) ≥ g(x) означает нахождение значений переменной х, при которых график функции f(x) лежит выше графика функции g(x). Для этого всегда необходимо найти точки пересечения графиков (если они существуют).

Пример 1.

Решить неравенство |x + 5| < bx.

Решение.

Строим графики функций у = |x + 5| и у = bx (рис. 2) . Решением неравенства будут те значения переменной х, при которых график функции у = |x + 5| будет находиться ниже графика функции у = bx.

На рисунке видно:

1) При b > 1 прямые пересекаются. Абсцисса точки пересечения графиков этих функций есть решение уравнения х + 5 = bx, откуда х = 5/(b – 1). График у = bx находится выше при х из интервала (5/(b – 1); +∞), значит это множество и есть решение неравенства.

2) Аналогично находим, что при -1 < b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).

3) При b ≤ -1 x € (-∞; 5/(b – 1)).

4) При 0 ≤ b ≤ 1 графики не пересекаются, а значит, и решений у неравенства нет.

Ответ: x € (-∞; 5/(b – 1)) при b ≤ -1;
x € (-5/(b + 1); 5/(b – 1)) при -1 < b < 0;
решений нет при 0 ≤ b ≤ 1; x € (5/(b – 1); +∞) при b > 1.

Пример 2.

Решить неравенство а(а + 1)х > (a + 1)(a + 4).

Решение.

1) Найдем «контрольные » значения для параметра а: а 1 = 0, а 2 = -1.

2) Решим данное неравенство на каждом подмножестве действительных чисел: (-∞; -1); {-1}; (-1; 0); {0}; (0; +∞).

a) a < -1, из данного неравенства следует, что х > (a + 4)/a;

b) a = -1, тогда данное неравенство примет вид 0·х > 0 – решений нет;

c) -1 < a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0, тогда данное неравенство имеет вид 0 · х > 4 – решений нет;

e) a > 0, из данного неравенства следует, что х > (a + 4)/a.

Пример 3.

Решить неравенство |2 – |x|| < a – x.

Решение.

Строим график функции у = |2 – |x|| (рис. 3) и рассматриваем все возможные случаи расположения прямой у = -x + а.

Ответ: решений у неравенства нет при а ≤ -2;
x € (-∞; (а – 2)/2) при а € (-2; 2];
x € (-∞; (a + 2)/2) при a > 2.

При решении различных задач, уравнений и неравенств с параметрами открывается значительное число эвристических приемов, которые потом с успехом могут быть применены в любых других разделах математики.

Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры. Именно поэтому, овладев методами решения задач с параметрами, вы успешно справитесь и с другими задачами.

Остались вопросы? Не знаете, как решать неравенства?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.