Содержание

Введение

Понятие фрактала.........................................................................................4

История появления фракталов………………………………………........6

Алгебраические фракталы………………..……………………………….8

1. Множество Мальдеброда……………………………………………...9

   Множество Жюлиа……………………………………………………11

   Бассейны (фракталы) Ньютона………………………………………13

   Фрактал (пузыри) Галлея……………………………………………..14

Практическое применение фракталов…………………………………...15

Заключение……………………………………………………………………….19

Список используемой литературы…………………………………………...…20

Введение

Язык науки стремительно меняется в современном мире. История развития физики насчитывает уже не одно столетие. За это время изучено огромное количество разнообразных явлений природы, открыты фундаментальные законы физики, объясняющие различные экспериментальные факты.

Большинство систем в природе сочетают два свойства: во-первых, они очень велики, часто многогранны, многообразны и сложны, а во- вторых они формируются под действием очень небольшого количества простых закономерностей, и далее развиваются, подчиняясь этим простым закономерностям. Это самые разные системы, начиная от кристаллов и просто кластеров (различного рода скоплений, таких как облака, реки, горы, материки, звёзды), заканчивая экосистемами и биологическими объектами (от листа папоротника до человеческого мозга). Фракталы являются как раз такими объектами: с одной стороны - сложные (содержащие бесконечно много элементов), с другой стороны - построенные по очень простым законам. Благодаря этому свойству, фракталы обнаруживают много общего со многими природными объектами. Но фрактал выгодно отличается от природного объекта тем, что фрактал имеет строгое математическое определение и поддаётся строгому описанию и анализу. Поэтому теория фракталов позволяет предсказать скорость роста корневых систем растений, трудозатраты на осушение болот, зависимость массы соломы от высоты побегов и многое другое. Это новое направление в математике, совершившее в научной парадигме переворот, сравнимый по значимости с теорией относительности и квантовой механикой. Объекты фрактальной геометрии по своему внешнему виду резко отличаются от привычных нам "правильных" геометрических фигур. Фактически, это прорыв в математическом описании систем, которые на протяжении долгого времени такому описанию не поддавались.

Фрактальная геометрия не есть "чистая" геометрическая теория. Это скорее концепция, новый взгляд на хорошо известные вещи, перестройка восприятия, заставляющая исследователя по новому видеть мир.

Целью моей работы является ознакомление с понятием «фрактал» и его разновидностью «алгебраический фрактал».

Понятие фрактала

Сравнительно недавно в математике возник образ объекта, более объемистого, но тем не менее сходного с линией. Некоторым ученым было трудно примириться с понятием линии, не имеющей ширины, поэтому постепенно ими стали изучаться геометрические формы и структуры, имеющие дробную пространственную размерность. На смену непрерывным кривым, обладающим всеми своими производными, пришли ломаные или очень изрезанные кривые. Ярким примером такой кривой является траектория броуновской частицы. Так в науке возникло понятие фрактала.

Фрактал (лат. fractus - дробленый, сломанный, разбитый) - сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком (рис. 1). В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность.

Рис. 1
Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими – либо из перечисленных ниже свойств:

Обладает нетривиальной структурой на всех шкалах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.

Является самоподобной или приближённо самоподобной.

Обладает дробной метрической размерностью.

Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, кровеносная система и система альвеол человека или животных.
Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.

История появления фракталов

Изучение фракталов на рубеже XIX и XX веков носило скорее эпизодический, нежели систематический характер, потому что раньше математики в основном изучали «хорошие» объекты, которые поддавались исследованию при помощи общих методов и теорий. В 1872 году немецкий математик Карл Вейерштрасс построил пример непрерывной функции, которая нигде не дифференцируема, то есть не имеет касательной ни в одной своей точке. Однако его построение было целиком абстрактно и трудно для восприятия. Поэтому в 1904 году швед Хельге фон Кох придумал такую непрерывную кривую, которая нигде не имеет касательной, причем ее довольно просто нарисовать. Оказалось, что она обладает свойствами фрактала. Один из вариантов этой кривой носит название «снежинка Коха».
Идеи самоподобия фигур подхватил француз Поль Пьер Леви, будущий наставник Бенуа Мандельброта. В 1938 году вышла его статья «Плоские и пространственные кривые и поверхности, состоящие из частей, подобных целому», в которой описан еще один фрактал – С-кривая Леви. Все эти вышеперечисленные фракталы можно условно отнести к одному классу конструктивных (геометрических) фракталов.
Другой класс – динамические (алгебраические) фракталы, к которым относится множество Мандельброта. Первые исследования в этом направлении начались в начале XX века и связаны с именами французских математиков Гастона Жулиа и Пьера Фату. В 1918 году была опубликована работа Жулиа, посвященная итерациям комплексных рациональных функций, в которой описаны множества Жулиа – целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно

Первые идеи фрактальной геометрии возникли в 19 веке. Кантор с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек (так называемая Пыль Кантора). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками. (Рис. 2)

Рис. 2

Пеано нарисовал особый вид линии.(Рис. 3)

Рис. 3

Для ее рисования Пеано использовал следующий алгоритм.

На первом шаге он брал прямую линию и заменял ее на 9 отрезков длиной в 3 раза меньшей, чем длина исходной линии (часть 1 и 2 рисунка). Далее он делал то же самое с каждым отрезком получившейся линии. И так до бесконечности. Уникальность линии в том, что она заполняет всю плоскость. Доказано, что для каждой точки на плоскости можно найти точку, принадлежащую линии Пеано.

Кривая Пеано и пыль Кантора выходили за рамки обычных геометрических объектов. Они не имели четкой размерности. Пыль Кантора строилась вроде бы на основании одномерной прямой, но состояла из точек (размерность 0). А кривая Пеано строилась на основании одномерной линии, а в результате получалась плоскость. Во многих других областях науки появлялись задачи, решение которых приводило к странным результатам, на подобие описанных выше (Броуновское движение, цены на акции).

Вплоть до 20 века шло накопление данных о таких странных объектах, без какой - либо попытки их систематизировать. Так было, пока за них не взялся Бенуа Мандельброт – отец современной фрактальной геометрии и слова фрактал. Постепенно сопоставив факты, он пришел к открытию нового направления в математике – фрактальной геометрии.

Чтобы представить себе фрактал понаглядней рассмотрим пример, приведенный в книге Б.Мандельброта “The Fractal Geometry of Nature” (“Фрактальная геометрия природы”) ставший классическим – “Какова длина берега Британии?”. Ответ на этот вопрос не так прост, как кажется. Все зависит от длины инструмента, которым пользуются. Померив берег с помощью километровой линейки полуают какую-то длину. Однако пропускают много небольших заливчиков и полуостровков, которые по размеру намного меньше измеряемой линейки. Уменьшая размер линейки до 1 метра – получается, что длина берега станет больше. Измеряя длину берега с помощью миллиметровой линейки, учитывая детали, которые больше миллиметра, длина будет еще больше. В итоге ответ на такой, казалось бы, простой вопрос может поставить в тупик кого угодно – длина берега Британии бесконечна.

Алгебраические фракталы

Свое название алгебраические фракталы получили за то, что их строят, на основе алгебраических формул. Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный расчет функции, где z - комплексное число, а f некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится - на экран выводится точка. При этом значения функции для разных точек комплексной плоскости может иметь разное поведение:

с течением времени стремится к бесконечности;

стремится к 0;
принимает несколько фиксированных значений и не выходит за их пределы;
поведение хаотично, без каких либо тенденций.

3.1 Множество Мандельброта

Множество Мандельброта (один из самых известных фрактальных объектов) впервые было построено (визуально с применением ЭВМ) Бенуа Мандельбротом весной 1980 г. в исследовательском центре фирмы IBM им. Томаса Дж. Уотсона. И хотя исследования подобных объектов начались ещё в прошлом веке, именно открытие этого множества и совершенствование аппаратных средств машинной графики в решающей степени повлияли на развитие фрактальной геометрии и теории хаоса. Итак, что же такое множество Мандельброта.

Рассмотрим функцию комплексного переменного . Положим и рассмотрим последовательность , где для любого . Такая последовательность может быть ограниченной (т.е. может существовать такое r, что для любого ) либо "убегать в бесконечность" (т.е. для любого r > 0существует ). Множество Мандельброта можно определить как множество комплексных чисел c, для которых указанная последовательность является ограниченной. К сожалению, не известно аналитического выражения, которое позволяло бы по данному c определить, принадлежит ли оно множеству Мандельброта или нет. Поэтому для построения множества используют компьютерный эксперимент: просматривают с некоторым шагом множество точек на комплексной плоскости, для каждой точки проводят определённое число итераций (находят определённое число членов последовательности) и смотрят за её "поведением". (Рис. 4).

Доказано, что множество Мандельброта размещается в круге радиуса r=2 с центром в начале координат. Таким образом, если на некотором шаге модуль очередного члена последовательности превышает 2, можно сразу сделать вывод, что точка, соответствующая c, определяющему данную последовательность, не принадлежит множеству Мандельброта.

Уменьшая шаг, с которым просматриваются комплексные числа, и увеличивая количество итераций, мы можем получать сколь угодно подробные, но всегда лишь приближённые изображения множества.

Пусть в нашем распоряжении имеется N цветов, занумерованных для определённости от 0 до N-1. Будем считать, опять же для определённости, что черный цвет имеет номер 0. Если для данного c после N-1 итераций точка не вышла за круг радиуса 2, будем считать, что c принадлежит множеству Мандельброта, и покрасим эту точку c в чёрный цвет. Иначе, если на некотором шаге k (k Є ) очередная точка вышла за круг радиуса 2 (т.е. на k-ом шаге мы поняли, что она "убегает"), покрасим её в цвет k.

Красивые изображения получаются при удачном выборе палитры и окрестности множества (а именно вне множества мы и получим "цветные точки). (Рис. 5, 6).

Рис. 4

Рис. 5 Рис. 6

3.2 Множество Жюлиа

Множества Жюлиа, тесно связанные с множеством Мандельброта, были исследованы ещё в начале XX века математиками Гастоном Жюлиа и Пьером Фату (см. ). В 1917-1919 гг. ими были получены основополагающие результаты, связанные с итерированием функций комплексного переменного. Вообще говоря, этот факт заслуживает отдельного обсуждения и является впечатляющим примером математического исследования, на многие десятилетия опередившего время (учёные могли лишь приблизительно представлять, как выглядят исследуемые ими объекты!), но мы опишем лишь способ построения множеств Жюлиа для функции комплексного переменного . Говоря более точно, мы будем строить т.н. "заполняющие множества Жюлиа".

Рассмотрим прямоугольник (x 1 ;y 1 )-(x 2 ;y 2 ). Зафиксируем константу c и станем просматривать точки выбранного прямоугольника с некоторым шагом. Для каждой точки, как и при построении множества Мандельброта, проведём серию итераций (чем больше число итераций, тем точнее будет получено множество). Если после серии итераций точка не "убежала" за границу круга радиуса 2, поставим её чёрным цветом, иначе цветом из палитры. (Рис. 7, 8, 9, 10).

Рис. 7

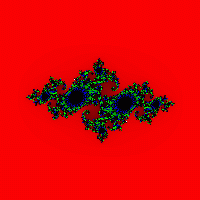
Рис.8 Рис. 9

Рис. 10

3.3 Бассейны (фракталы) Ньютона

Еще один тип динамических фракталов составляют фракталы (так называемые бассейны) Ньютона. (Рис. 11). Формулы для их построения основаны на методе решения нелинейных уравнений, который был придуман великим математиком еще в XVII веке. Применяя общую формулу метода Ньютона zn+1 = zn - f (zn)/f"(zn), n=0, 1, 2… для решения уравнения f (x)=0 к многочлену zk-a, получим последовательность точек: zn+1 = (k-1)znk/kznk-1, n=0, 1, 2… Выбирая в качестве начальных приближений различные комплексные числа z0, будем получать последовательности, которые сходятся к корням этого многочлена. Поскольку корней у него ровно k, то вся плоскость разбивается на k частей - областей притяжения корней. Границы этих частей имеют фрактальную структуру.

Рис. 11

3.4 Фрактал (пузыри) Галлея

Такие фракталы получаются, если в качестве правила для построения динамического фрактала использовать формулу Галлея для поиска приближенных значений корней функции. (Рис. 12).

Метод состоит из последовательности итераций:

Идея метода почти та же, что используется для рисования динамических фракталов: берем какое-нибудь начальное значение (как обычно, здесь речь идет о значениях переменных и функций) и применяем к нему много раз формулу, получая последовательность чисел. Почти всегда она сходится к одному из нулей функции (то есть значению переменной, при котором функция принимает значение 0). Метод Галлея, несмотря на громоздкость формулы, работает эффективнее метода : последовательность сходится к нулю функции быстрее.

Рис. 12

Практическое применение фракталов

Фракталы находят всё большее применение в науке. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Вот несколько примеров.

Компьютерные системы

Cреди всех картинок, которые может создавать компьютер, лишь немногие могут поспорить с фрактальными изображениями, когда идет речь о подлинной красоте.

Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого вида сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом, картинки сжимаются гораздо лучше, чем это делается обычными методами(такими как jpeg или gif). Другое преимущество фрактального сжатия в том, что при увеличении картинки, не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него.

Механика жидкостей

Изучение турбулентности в потоках очень хорошо подстраивается под

фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных потоков.

При помощи фракталов также можно смоделировать языки пламени.

Пористые материалы хорошо представляются во фрактальной форме в связи с тем, что они имеют очень сложную геометрию. Это используется в нефтяной науке.

Телекоммуникации

Для передачи данных на расстоянии используются антенны, имеющие

фрактальные формы, что сильно уменьшает их размеры и вес. Фракталы используются для описания кривизны поверхностей. Неровная поверхность характеризуется комбинацией из двух разных фракталов.
Медицина

Биосенсорные взаимодействия. Биение сердца.
Биология

Моделирование хаотических процессов, в частности при описании моделей популяции.
Нанотехнологии

В случае нанотехнологии фракталы тоже играют важную роль, поскольку из-за своей иерархической самоорганизации многие наносистемы обладают нецелочисленной размерностью, то есть являются по своей геометрической, физико-химической или функциональной природе фракталами. Например, ярким примером химических фрактальных систем являются молекулы « дендримеров » . (Рис. 13)

Рис. 13

Литература

Среди литературных произведений находят такие, которые обладают текстуальной, структурной или семантической фрактальной природой. В текстовых фракталах потенциально бесконечно повторяются элементы текста («У попа была собака…», «Притча о философе, которому снится, что он бабочка, которой снится, что она философ, которому снится…» и тексты с наращениями («Дом, который построил Джек»)

В структурных фракталах схема текста потенциально фрактальна: венок сонетов (15 стихотворений), венок венков сонетов (211 стихотворений), венок венков венков сонетов (2455 стихотворений).

Заключение

Фрактал - объект, обладающий бесконечной сложностью, позволяющий рассмотреть столько же своих деталей вблизи, как и издалека. Земля -классический пример фрактального объекта. Из космоса она выглядит как шаp. Если приближаться к ней, мы обнаружим океаны, континенты, побережья и цепи гор. Будем рассматривать горы ближе - станут видны еще более мелкие детали: кусочек земли на поверхности горы в своем масштабе столь же сложный и неровный, как сама гора. И даже еще более сильное увеличение покажет крошечные частички грунта, каждая из которых сама является фрактальным объектом.

В заключении хочется сказать, что после того как были открыты фракталы, для многих учёных стало очевидно, что старые, добрые формы евклидовой геометрии сильно проигрывают большинству природных объектов из-за отсутствия в них некоторой нерегулярности, беспорядка и непредсказуемости. Возможно, что новые идеи фрактальной геометрии помогут изучить многие загадочные явления окружающей природы. В настоящие время фракталы стремительно вторгаются во многие области физики, биологии, медицины, социологии, экономики. Методы обработки изображений и распознавания образов, использующие новые понятия, дают возможность исследователям применить этот математический аппарат для количественного описания огромного количества природных объектов и структур.

Список используемой литературы

1. Bведение во фракталы,

2. Жиков В. В. О множествах Жюлиа. // Современное естествознание: Энциклопедия: В 10 т. Т.1: Математика. Механика. М., 2000.

3. Жиков В. В. Фракталы. // Современное естествознание: Энциклопедия: В 10 т. Т.1: Математика. Механика. М., 2000.

4. Мандельброт Б. Фрактальная геометрия природы. – М: Институт компьютерных исследований, 2002.

5. Морозов А.Д. Введение в теорию фракталов.-Москва-Ижевск: Институт компьютерных исследований, 2002, 160стр.

6. Динамические (алгебраические) фракталы // Элементы. . URL: http :// elementy . ru / posters / fractals / dynamic

7. Динамические (алгебраические) фракталы // Элементы. . URL: http :// elementy.ru/posters/fractals/Mandelbrot#nop

8. Алгебраические фракталы // Фракталы. . URL: http://rusproject.narod.ru/article/fractals.htm

Бабочки, конечно, ничего не знают о змеях. Зато о них знают птицы, охотящиеся на бабочек. Птицы, плохо распознающие змей, чаще становятся...

Если octo на латыни «восемь», то почему октава содержит семь нот?

Октавой называется интервал между двумя ближайшими одноименными звуками: до и до, ре и ре и т. д. С точки зрения физики «родство» этих...

Почему важных особ называют августейшими?

В 27 году до н. э. римский император Октавиан получил титул Август, что на латыни означает «священный» (в честь этого же деятеля, кстати,...

Чем пишут в космосе

Известная шутка гласит: «NASA потратило несколько миллионов долларов, чтобы разработать специальную ручку, способную писать в космосе....

Почему основа жизни - углерод?

Известно порядка 10 миллионов органических (то есть основанных на углероде) и лишь около 100 тысяч неорганических молекул. Вдобавок...

Почему кварцевые лампы синие?

В отличие от обычного стекла, кварцевое пропускает ультрафиолет. В кварцевых лампах источником ультрафиолета служит газовый разряд в парах ртути. Он...

Почему дождь иногда льет, а иногда моросит?

При большом перепаде температур внутри облака возникают мощные восходящие потоки. Благодаря им капли могут долго держаться в воздухе и...

В главах 6 и 7, призвав на помощь геоморфологию, мы ввели кривые Коха и Пеано, однако объекты наиболее значительных приложений теории фракталов находятся в несколько иных областях. Неспешно подбираясь к основным течениям в науке, мы рассмотрим в этой главе (и в двух последующих) два вопроса исключительной древности, важности и сложности.

Распределение звезд, галактики, скопления галактик и тому подобные материи издавна завораживают как любителей, так и специалистов, однако кластеризация до сих пор остается на периферии астрономии, да и всей астрофизики в целом. Главная причина заключается в том, что никто так и не в состоянии объяснить, почему распределение материи подчиняется иррегулярным иерархическим законам - по крайней мере, в определенном диапазоне масштабов. Во многих трудах, посвященных этой теме, можно встретить упоминание о феномене кластеризации, однако в серьезных теоретических исследованиях ее, как правило, поспешно заметают под ковер, утверждая, что галактики распределены вполне однородно - в масштабе, превышающем некий большой, но неопределенный порог.

Рассматривая ситуацию с менее фундаментальных позиций, можно сказать, что нежелание иметь дело с иррегулярным проистекает из отсутствия инструментов для его математического описания. От статистики требуется выбрать между двумя допущениями, из которых только одно можно счесть тщательно исследованным (асимптотическую однородность). Стоит ли удивляться, что результаты, мягко говоря, неубедительны?

Вопросы, однако, таковы, что от них трудно отмахнуться. Я считаю совершенно необходимым - параллельно с продолжением попыток объяснить кластеризацию - найти способ описать ее и смоделировать реальность чисто геометрическими средствами. Рассматривая эту тему с фрактальных позиций на протяжении нескольких глав настоящего эссе, мы рассчитываем с помощью недвусмысленных моделей показать, что полученные свидетельства предполагают такую степень кластеризации, которая далеко выходит за пределы, поставленные для нее существующими моделями.

Эту главу следует считать вводной: здесь мы познакомимся с одной весьма влиятельной теорией образования звезд и галактик, предложенной Хойлом, с основной формальной моделью их распределения, которой мы обязаны Фурнье д"Альбу (эта модель также известна как модель Шарлье), и, что самое важное, получим некоторые эмпирические данные. Мы покажем, что и теорию, и данные можно интерпретировать в рамках понятия о масштабно-инвариантной фрактальной пыли. Я настаиваю на том, что распределение галактик и звезд включает в себя некую зону самоподобия, внутри которой фрактальная размерность удовлетворяет неравенству . Кроме того, здесь вкратце изложены теоретические причины, согласно которым можно ожидать , и, как следствие, обсуждается вопрос, почему наблюдаемая величина составляет .

Анонс. В главе 22 мы воспользуемся фрактальными инструментами для улучшения нашего понимания смысла космологического принципа, рассмотрим, как его можно и нужно модифицировать, и узнаем, почему такая модификация непременно требует случайности. Обсуждение скоплений в рамках усовершенствованной модели мы отложим до глав 22, 23 и с 32 по 35.

МОЖНО ЛИ ГОВОРИТЬ О ГЛОБАЛЬНОЙ плотности МАТЕРИИ?

Начнем с тщательного рассмотрения концепции глобальной плотности материи. Как и в случае береговых линий, здесь все, на первый взгляд, выглядит очень простым, однако на деле очень быстро - и весьма интересно - запутывается. Для определения и измерения плотности начинают с массы , сосредоточенной внутри сферы радиуса с центром, совпадающим с центром Земли. Так оценивается приблизительная плотность, определяемая как

.

После этого величину устремляют к бесконечности, а глобальная плотность определяется как предел, к которому сходится в этом случае приблизительная плотность.

Однако обязательно ли глобальная плотность сходится к положительному и конечному пределу? Если так, то скорость такого схождения оставляет желать лучшего, и это еще мягко сказано. Более того, оцеки предельной плотности, будучи рассмотрены во временной перспектив ведут себя довольно странно. По мере того как увеличивалась глубина наблюдаемой в телескоп Вселенной, приблизительная плотность на удивление систематически уменьшалась. Согласно де Вокулеру , уменьшение всегда было . Наблюдаемый показатель мно меньше 3 - в наилучшем приближении .

Де Вокулер выдвинул тезис о том, что поведение величины приблизительной плотности отражает реальность, имея в виду, что . Эта формула вызывает в памяти классический результат для шара радиуса , вложенного в евклидово пространство размерности , - объем такого шара . В главе 6 мы встречались с такой же формуле для кривой Коха, с той лишь разницей, что показателем там была не евклидова размерность , а дробная фрактальная размерность. А в главе 8 мы получили формулу для канторовой пьи на временной оси (здесь ).

Все эти прецеденты заставляют (причем весьма настойчиво) предположить, что показатель де Вокулера представляет собой не что иное, как фрактальную размерность.

ВХОДЯТ ЛИ ЗВЕЗДЫ В ДИАПАЗОН МАСШТАБНОЙ ИНВАРИАНТНОСТИ?

Очевидно, что диапазон масштабной инвариантности, в котором удовлетворяет неравенству , не должен включать в себя объекты с явно определенными границами - такие, например, как планеты. А вот входят ли в него звезды? Согласно данным, полученным Уэбби ком и приведенным в , массу Млечного Пути внутри сферы рад уса вполне можно представить в виде , где величина экстраполируется с галактик. Мы, однако, продолжим наше обсуждение исключительно в галактических терминах.

СУЩЕСТВУЕТ ЛИ У ДИАПАЗОНА МАСШТАБНОЙ ИНВАРИАНТНОСТИ ВЕРХНИЙ ПОРОГ?

Вопрос о том, насколько далеко в сторону очень больших масштабов простирается диапазон, внутри которого , весьма противоречив, причем в последнее время он снова привлек к себе внимание. Многие авторы либо прямо заявляют, либо подразумевают, что этот диапазон допускает существование внешнего предела, соответствующего размерам скоплений галактик. Другие авторы выражают свое несогласие с этим мнением. Де Вокулер утверждает, что «кластеризация галактик и, возможно, всех остальных форм материи является доминатной характеристикой структуры Вселенной во всех доступных наблюдению масштабах, причем нет никаких указаний на какое бы то ни было приближение к однородности; средняя плотность вещества неуклонно падает по мере того, как принимаются во внимание все большие объемы пространства, и у нас нет экспериментально подтвержденных оснований полагать, что эта тенденция не распространяется на значительно большие расстояния и меньшие значения плотности».

Дебаты между этими двумя школами, безусловно, весьма интересны и важны - для космологии, но не для нашего эссе. Даже если диапазон, в котором , имеет границы с обеих сторон, само его существование достаточно значительно для того, чтобы оправдать самое тщательное исследование.

В любом случае Вселенная (совсем как тот клубок ниток, о котором мы говорили в главе 6) располагает, по всей видимости, целым рядом различных эффективных размерностей. Если начать с масштабов порядка радиуса Земли, то первой встретившейся нам размерностью будет 3 (такова размерность твердых тел с четкой границей). Далее размерность падает до 0 (так как материя рассматривается как скопление изолированных точек). Далее идет весьма интересный участок, характеризуемый некой нетривиальной размерностью, удовлетворяющей неравенству . Если масштабно-инвариантная кластеризация продолжается до бесконечности, то на этом последнем значении ряд эффективных размерностей и заканчивается. Если же существует конечный внешний порог, то к списку добавляется четвертый интервал размерностей, внутри которого точки теряют свою индивидуальность, и у нас на руках оказывается однородный газ, т. е. размерность снова возвращается к 3.

Самым же наивным представлением является то, согласно которому галактики распределены во Вселенной приблизительно однородно. В этом случае последовательность размерностей D сводится к трем значениям: 3, 0 и опять 3.

< Общая теория относительности утверждает, что при отсутствии материи локальная геометрия пространства стремится стать плоской и евклидовой, в то время как присутствие материи переводит ее в локально риманову. Здесь мы можем говорить о глобально плоской Вселенной, размерность которой равна 3 с локальными значениями . Такой тип возмущений описан в , довольно туманной работе, автор которой приводит (с. 312) пример построения кривой Коха (см. главу 6), не ссылаясь при этом на самого Коха.

ВСЕЛЕННАЯ ФУРНЬЕ

Нам остается лишь построить фрактал, который удовлетворял бы правилу , и посмотреть, как он будет согласовываться с общепринятыми взглядами на Вселенную. Первая подробно описанная модель такого рода была предложена Э. Э. Фурнье д"Альбом (см. главу 40). Хотя книга Фурнье представляет собой по большей части художественный вымысел, замаскированный под научное исследование, в ней все же содержится несколько чрезвычайно интересных соображений, которые мы вскоре обсудим. Сначала же, как мне кажется, следует описать структуру, предложенную Фурнье.

Начинаем построение с правильного восьмигранника, проекция которого представлена в центре рис. 141. Проекция показывает четыре угла квадрата, диагональ которого составляет 12 «единиц», и центр этого квадрата. Однако у восьмигранника есть еще две точки над и под нашей плоскостью на перпендикуляре, проведенном через центр квадрата, на одинаковом расстоянии в 6 «единиц» от этого центра.

Далее каждая точка заменяется шаром радиуса 1, который мы будем рассматривать как «звездный агрегат нулевого порядка». Наименьший шар, содержащий в себе все 7 первоначальных шаров, назовем «звездным агрегатом первого порядка». Агрегат второго порядка получается увеличением агрегата первого порядка в раз и заменой каждого из новых шаров радиуса 7 копией агрегата первого порядка. Аналогичным образом, агрегат третьего порядка получается увеличением агрегата второго порядка в раз и заменой каждого из шаров копией агрегата второго порядка. И так далее.

Короче говоря, при переходе между соседними порядками агрегации как число точек, так и радиус шаров увеличивается в раз. Следовательно, для всякого значения , которое является радиусом какого-либо агрегата, функция , определяющая количество точек, содержащихся в шаре радиуса , имеет вид . Для промежуточных функция принимает меньшие значения (достигая ), однако, согласно общей тенденции, .

Возможно также интерполировать агрегаты нулевого порядка последовательными этапами до агрегатов порядка -1, -2 и т. д. На первом этапе заменим каждый агрегат нулевого порядка копией агрегата первого порядка, уменьшенной в отношении 1/7, и так далее. При таком построении отношение остается истинным для все меньших значений . После бесконечной экстра- и интерполяции мы получаем самоподобное множество размерности .

Кроме того, размерность объекта в 3-пространстве вовсе не обязывает его непременно быть прямой линией да и любой другой спрямляемой кривой. Ему даже не обязательно быть связным. Каждая размерность совместима с любой меньшей либо равной по величине топологической размерностью. В частности, топологическая размерность бесконечной в обе стороны вселенной Фурнье равна 0, так как она является вполне несвязной «пылью».

РАСПРЕДЕЛЕНИЕ МАССЫ: ФРАКТАЛЬНАЯ ГОМОГЕННОСТЬ

Шаг от геометрии к распределению массы представляется мне как нельзя более очевидным. Если каждый звездный агрегат нулевого порядка нагрузить единичной массой, то масса внутри шара радиуса идентична величине , а следовательно, . Кроме того, чтобы получить агрегаты порядка -1 из агрегатов нулевого порядка, необходимо разбить шар, который мы считали однородным и обнаружить, что он состоит из семи меньших шаров. На этом этапе правило распространяется и на радиусы, меньшие единицы.

Рассматривая полученное распределение массы по всему 3-пространству, мы видим, что оно чрезвычайно неоднородно, хотя на фрактале Фурнье ему в однородности нет равных. (Вспомните рис. 120.) В частности, любые две геометрически одинаковые части вселенной Фурнье содержат одинаковые массы. Предлагаю такое распределение массы называть фрактально гомогенным.

< Предыдущее определение сформулировано в терминах масштабно-инвариантных фракталов, но концепция фрактальной гомогенности в общем случае гораздо шире. Она применима к любому фракталу, для которого положительна и конечна хаусдорфова мера в размерности . Фрактальная гомогенность требует, чтобы масса, содержащаяся в множестве, была пропорциональна хаусдорфовой мере этого множества.

ВСЕЛЕННАЯ ФУРНЬЕ КАК КАНТОРОВА ПЫЛЬ. РАСШИРЕНИЕ Д0

Я надеюсь, что читателя не сбило с толку небрежное употребление фрактальной терминологии в начальных разделах этой главы. Очевидно, что Фурнье, сам того не осознавая, шел путем, параллельным пути своего современника Кантора. Основная разница заключается в том, что конструкция Фурнье вложена в пространство, а не в интервал на прямой. Для вящего усиления сходства достаточно заменить шарообразные агрегаты Фурнье на блоки (заполненные кубы). Каждый агрегат нулевого порядка становится блоком, длина стороны которого равна 1, и включает в себя 7 меньших агрегатов со стороной 1/7: центр одного из них совпадает с центром исходного куба, а остальные шесть касаются центральных подквадратов на гранях исходного куба.

Ниже мы рассмотрим, как получил значение из фундаментального физического феномена Фурнье, и как к тому же результату пришел Хойл. С геометрической же точки зрения, случай является особым, даже если на протяжении всего построения придерживаться формы восьмигранника и значения . Так как шары не перекрывают друг друга, величина может принимать любое значение в интервале от 3 до бесконечности, в результате чего получаем закон , где на всем интервале от 0 до .

МОДЕЛЬ ШАРЛЬЕ И ДРУГИЕ ФРАКТАЛЬНЫЕ ВСЕЛЕННЫЕ

Вышеописанные построения не избежали ни одного из недостатков, характерных для первых фрактальных моделей. Сильнее всего бросается в глаза то, что модель Фурнье, подобно модели кривой Коха в главе 6 и модели канторовой пыли в главе 8, до гротескности правильна. Для исправления ситуации Шарлье предложил предоставить и возможность переходить с одного иерархического уровня на другой, принимая значения и .

Репутация Шарлье в научных кругах была столь высока, что, несмотря на все его щедрые похвалы Фурнье, высказанные на всех ведущих языках науки того времени, даже исходную модель вскоре стали приписывать знаменитому интерпретатору, а не никому не известному автору. Новая модель широко обсуждалась в то время, особенно в . Более того, она привлекла внимание весьма влиятельного Эмиля Бореля, чьи комментарии в очень проницательны, хотя и несколько суховаты. Однако с той поры, если не считать нескольких судорожных попыток вытащить ее на свет, модель Шарлье пребывает в забвении (не очень убедительные причины такого забвения изложены в , с. 20-22 и 408-409). Тем не менее, умирать она упорно не желает. Основная идея к сегодняшнему дню была уже много раз открыта разными исследователями независимо друг от друга, особенно рекомендую заглянуть в . (А еще см. раздел ПОЛЬ ЛЕВИ в главе 40.) Наиболее важным я, однако, считаю тот факт, что фрактальная основа вселенной Фурнье имплицитно присутствует в рассуждениях о турбулентности и галактиках в работе (см. главу 10) и в модели галактического генезиса, предложенной Хойлом в (ее мы рассмотрим чуть ниже).

Главная фрактальная составляющая присутствует и в моих моделях (см. главы с 32 по 35).

В этом свете возникает вопрос: может ли модель распределения галактик не быть фракталом с одним или двумя порогами? Думаю, что нет. Если мы согласны с тем, что распределение должно быть масштабно-инвариантным (причины необходимости этого изложены в главе 11), и с тем, что множество, на котором концентрируется материя, не является стандартным масштабируемым множеством, у нас не остается иного выбора, кроме признания фрактальности этого множества.

Принимая во внимание важность масштабной инвариантности, нетрудно понять, почему немасштабируемое обобщение Шарлье модели Фурнье было с самого начала обречено. < Оно, кстати, позволяет величине изменяться в зависимости от то в пределах двух границ, и . Вот и еще одна тема для обсуждения: эффективная размерность не обязательно должна иметь одно-единственное значение, это значение может плавать между верхним и нижним пределами. К этой теме мы еще вернемся в главе 15.

ПОЧЕМУ ФУРНЬЕ ОЖИДАЛ D = 1?

Обсудим теперь весьма впечатляющую аргументацию, которая привела Фурнье к выводу, что показатель должен быть равен 1 (см. , с. 103). Эта аргументация сама по себе является серьезным доводом в пользу того, чтобы имя ее автора не было забыто.

Рассмотрим галактический агрегат произвольного порядка с массой и радиусом . Отбросив бесплодные сомнения и применив к данному случаю формулу для объектов, обладающих сферической симметрией, допустим, что гравитационный потенциал на поверхности сферы равен ( - гравитационная постоянная). Звезда, падающая на нашу Вселенную, сталкивается с ее поверхностью на скорости .

Согласно Фурнье, из того факта, что ни одна доступная наблюдению звезда не движется со скоростью, превышающей 1/300 от скорости света, можно вывести очень важное заключение. Масса, содержащаяся внутри мирового шара, возрастает прямо пропорционально его радиусу, а не объему, или, иными словами, плотность вещества внутри мирового шара обратно пропорциональна площади его поверхности... Поясним последнее утверждение - потенциал на поверхности сферы всегда одинаков, так как он прямо пропорционален массе вещества внутри сферы и обратно пропорционален расстоянию от центра. Как следствие, звездные скорости, близкие к скорости света, не являются распространенным явлением в любой части Вселенной.

СТВОРАЖИВАНИЕ ПО ХОЙЛУ; КРИТЕРИЙ ДЖИНСА

Иерархическое распределение фигурирует и в теории Хойла (см. ), согласно которой галактики и звезды образуются посредством каскадного процесса, причем начинается этот процесс с однородного газа.

Рассмотрим газовое облако массы , нагретое до температуры и распределенное с однородной плотностью внутри шара радиуса . Как показал Джине, при возникает «критическая» ситуация. (Здесь - постоянная Больцмана, a - числовой коэффициент.) Находясь в критическом состоянии, первичное газовое облако нестабильно и неизбежно должно сжаться.

Хойл постулирует, что (а) величина достигает критического значения где-то в самом начале, (б) сжатие прекращается, когда объем газового облака уменьшается до 1 /25 от первоначального объема, и (в) каждое облако на этом этапе распадается на пять меньших облаков с одинаковыми размерами, массами и радиусами . То есть процесс приходит к тому же месту, на каком начался: результатом его является нестабильное состояние, за которым следует второй этап сжатия и разделения, затем - третий и т. д. Створаживание прекращается лишь тогда, когда облака становятся настолько непрозрачными, что задерживают образующееся при сжатии газа тепло внутри.

Как и в различных других областях, в которых встречаются подобные каскадные процессы, я предлагаю и к этому случаю применить общую терминологию, т. е. пять облаков мы будем называть творогом, а сам каскадный процесс - створаживанием. Как я уже упоминал при введении последнего термина, я просто не мог удержаться от аллюзий с галактиками.

Фурнье ради удобства графического изображения своей модели вводит , Хойл же утверждает, что физически обоснованным является значение . Детализация геометрической иллюстрации Фурнье выходит за всякие - разумные или необходимые - рамки. Высказывания Хойла относительно пространственной структуры творога, напротив, довольно туманны. Детальной реализации модели Хойла нам придется подождать до главы 23, где мы рассмотрим случайное створаживание. Как бы то ни было, упомянутые расхождения не имеют принципиального значения: главным является тот факт, что , т. е. показатель должен стать неотъемлемой частью нашего построения, если мы хотим, чтобы створаживание завершалось тем же состоянием, с которого оно начиналось, - а именно, нестабильностью Джинса.

Кроме того, если длительность первого этапа принять за 1, то, согласно данным по газовой динамике, длительность того этапа составит . Следовательно, общая длительность всего процесса, состоящего из бесконечного количества этапов, не превышает 1,2500.

ЭКВИВАЛЕНТНОСТЬ ПОДХОДОВ ФУРНЬЕ И ХОЙЛА К ВЫВОДУ D = 1

На границе нестабильного газового облака, удовлетворяющего критерию Джинса, скорость и температура связаны соотношением , так как равно и (Фурнье), и (Джине). Вспомним теперь о том, что в статистической термодинамике температура газа прямо пропорциональна среднеквадратической скорости его молекул. Значит, из комбинации критериев Фурнье и Джинса можно предположить, что на границе облака скорость падения макроскопического объекта прямо пропорциональна средней скорости его молекул. Тщательный анализ роли температуры в критерии Джинса непременно покажет, что эти два критерия эквивалентны. < Вероятнее всего, аналогия распространяется и на справедливость отношения внутри галактик, о чем сообщает Валленквист в .

ПОЧЕМУ D = 1, 23, А НЕ D = 1?

Расхождение между эмпирическим значением и теоретическим значением Фурнье и Хойла поднимает важную проблему. П. Дж. Э. Пиблс рассмотрел ее в 1974 г. с позиций теории относительности. В его труде получили исчерпывающее освещение физический и статистический (но не геометрический) аспекты упомянутой проблемы.

ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ НЕБА

Небо - это проекция Вселенной. Для получения этой проекции каждая точка Вселенной сначала описывается сферическими координатами , и , а затем координата заменяется на 1. Если Вселенная представляет собой фрактал с размерностью , а начало системы отсчета принадлежит этой самой Вселенной (см. главу 22), то структура проекции, как правило, определяется следующей альтернативой: подразумевает, что проекция покрывает некую ненулевую область неба, в то время как означает, что сама проекция имеет фрактальную размерность . < Как показано на рис. 141 и 143, «правило» не лишено исключений, обусловленных структурой фрактала и/или/ выбором точки отсчета. О таких правилах часто говорят «истинно с вероятностью 1».

ЗАМЕЧАНИЕ ПО ПОВОДУ ЭФФЕКТА ПЫЛАЮЩЕГО НЕБА (НЕВЕРНО НАЗЫВАЕМОГО ПАРАДОКСОМ ОЛЬБЕРСА)

Правило из предыдущего раздела имеет непосредственное отношение к мотивации, побуждавшей различных исследователей (включая Фурнье) открывать собственные варианты фрактальной Вселенной. Они понимали, что такие вселенные геометрически «отменяют» эффект пылающего неба, который еще часто (но неверно) называют парадоксом Олъберса. Если допустить, что распределение небесных тел равномерно (т. е. во всех масштабах), то небо над нами должно быть почти равномерно освещено и ночью, и днем, причем яркость этого освещения должна быть сравнима с солнечной.

Парадокс этот физиков больше не интересует, будучи сведен на нет теорией относительности, теорией расширяющейся Вселенной и другими соображениями. Однако его кончина имела занятный побочный эффект: многочисленные комментаторы принялись цитировать свои излюбленные объяснения эффекта пылающего неба - одни в надежде оправдаться за пренебрежительное отношение к кластеризации, другие же, напротив, напрочь отрицая ее реальность. Очень странная, надо сказать, точка зрения. Даже если предположить, что кластеризация галактик никак не связана с отсутствием эффекта пылающего неба, она все равно существует - и требует надлежащего изучения. К тому же, как мы увидим в главе 32, концепция расширяющейся Вселенной совместима не только со стандартной, но и с фрактальной гомогенностью.

Эффект пылающего неба объясняется очень просто. Поскольку количество излучаемого звездой света прямо пропорционально площади ее поверхности, количество света, достигающее наблюдателя, находящегося от звезды на расстоянии , должно быть , но площадь видимой поверхности звезды также . Таким образом, отношение количества света к видимому сферическому углу не зависит от . Кроме того, если распределение звезд во Вселенной равномерно, то практически любое направление взгляда рано или поздно встретит какую-нибудь звезду. Следовательно, небо освещено звездным светом равномерно и выглядит пылающим. (Лунный диск в этом случае образует исключительно темную область - по крайней мере, при отсутствии атмосферной диффузии.)

Если же допустить, что Вселенная фрактальна и что ее размерность , то парадокс разрешается сам собой. В этом случае проекция Вселенной на небесный свод является фрактальным множеством той же размерности , т. е. множеством нулевой площади. Даже если звезды имеют ненулевой радиус, большая часть направлений уходит в бесконечность, не встречая на своем пути ни одной звезды. Если смотреть вдоль этих направлений, то мы увидим только черноту ночного неба. Если за интервалом, в котором , следует интервал, в котором , то фон неба будет не строго черным, но чрезвычайно слабо освещенным.

На эффект пылающего неба обратил внимание еще Кеплер вскоре после того, как Галилей в «Звездном послании» благожелательно отозвался об идее безграничной Вселенной. В своей «Беседе со звездным посланцем» (1610) Кеплер высказал следующее возражение: «Нимало не колеблясь, Вы заявляете, что взгляду доступны более 10000 звезд... Если это так и если [звезды] той же природы, что и наше Солнце, то почему все эти солнца в совокупности не превосходят наше Солнце в яркости?... Может быть их затмевает эфир? Ни в малейшей степени... Совершенно очевидно, что наш мир никоим образом не может принадлежать беспорядочному рою из бесчисленных иных миров» (см. , с. 34-35).

Вывод был довольно спорный, однако об аргументации не забыли - свидетельством тому может служить замечание Эдмунда Галлея (сделанное им в 1720 г.): «Я слышал еще об одном возражении, которое гласит, что если бы число неподвижных звезд было более чем конечным, то весь свод их видимой сферы сплошь светился бы». Позднее это возражение обсуждалось де Шезо и И. Г. Ламбертом, однако авторство его приписали большому другу Гаусса немецкому астроному Ольберсу. Термин «парадокс Ольберса», которым с тех пор называют это противоречие, скандален, но симптоматичен. Результаты наблюдений, попавшие в разряд «не подлежащих классификации» (см. с. 51), часто приписываются первому же представителю Официального Большинства, который украсит их вполне классифицируемой оберткой, пусть даже и временной. Обсуждение предмета в исторической перспективе можно найти в .

ЗАМЕЧАНИЕ О НЬЮТОНОВСКОМ ТЯГОТЕНИИ

Преподобный Бентли все донимал Ньютона одним наблюдением, тесно связанным с эффектом пылающего неба: если распределение звезд однородно, то сила, с какой они действуют друг на друга, бесконечна. Можно добавить, что их гравитационный потенциал также бесконечен. И что любое распределение, в котором , даст при больших бесконечный потенциал во всех случаях, кроме . Современная теория потенциала (теория Фростмана) подтверждает тот факт, что между ньютоновским тяготением и значением существует некая особенная связь. Полученный Фурнье и Хойлом показатель также следует отнести к проявлениям этой связи. < Положение Фурнье о том, что «гравитационный потенциал на поверхности сферы всегда одинаков», является центральным в современной теории потенциала. ». Квадрат отношения скоростей, постулированный Фурнье, равен - как раз в середине упомянутого интервала.

АГГЛЮТИНИРОВАННАЯ ФРАКТАЛЬНАЯ ВСЕЛЕННАЯ?

Многие исследователи полагают, что можно объяснить образование звезд и других небесных объектов с помощью восходящего каскада (т. е. постепенной агглютинации сильно рассеянных частиц пыли во все большие куски), не желая ничего слышать о нисходящем каскаде а 1а Хойл (т. е. постепенной фрагментации очень больших и рассеянных масс на все меньшие части).

Похожая альтернатива возникает в связи с каскадами, постулированными в теории турбулентности (см. главу 10). Ричардсонов каскад протекает по нисходящей ко все более мелким вихрям, однако в процессе могут участвовать и восходящие каскады (см. главу 40, раздел ЛЬЮИС ФРАЙ РИЧАРДСОН). Таким образом, можно надеяться, что взаимоотношения между нисходящими и восходящими каскадами получат вскоре надлежащее объяснение.

ФРАКТАЛЬНЫЕ МАССИВЫ ТЕЛЕСКОПОВ

Вряд ли можно найти более подходящий завершающий штрих для этой дискуссии, чем замечание относительно инструментов, с помощью которых производится наблюдение галактик. Дайсон предлагает для улучшения качества наблюдения заменять большие одиночные телескопы массивами из малых телескопов. Диаметр каждого из малых телескопов должен составлять около 0,1м (размер наименьшего оптически существенного атмосферного возмущения), их центры должны образовывать фрактально иерархическую схему, а соединение между телескопами обеспечат интерферометры Карри. Грубый анализ приводит к выводу, что в качестве подходящего значения размерности следует взять 2/3. Вот заключение самого Дайсона: «Трехкилометровый массив из 1024 десятисантиметровых телескопов, соединенных между собой 1023 интерферометрами, - не самое практичное на сегодняшний день предложение. [Я выдвинул его] в качестве теоретической идеи, чтобы показать, что здесь, в принципе, можно сделать».

ОБЗОР СЛУЧАЙНЫХ ФРАКТАЛЬНЫХ МОДЕЛЕЙ СКОПЛЕНИЙ ГАЛАКТИК

Если верить тому, что можно эффективно описать распределение галактик с помощью нечаянно обнаруженных фрактальных моделей, не отличающихся ни сложностью, ни универсальностью, не стоит удивляться, что намеренно фрактальные случайные модели могут снабдить нас гораздо более эффективными описаниями. Начнем с того, что мы сможем значительно лучше понять створаживание Хойла, рассмотрев его в надлежащем окружении, т. е. среди случайных фракталов (см. главу 23). Еще большей значимостью обладают, на мой взгляд, разработанные мною случайные модели, о которых мы поговорим в главах с 32 по 35. Один из доводов в пользу рассмотрения нескольких моделей заключается в том, что за улучшение качества описания приходится «платить» возросшей сложностью. Второй довод - каждая модель строится на особой фрактальной пыли, каждая из которых заслуживает отдельного рассмотрения. Рассмотрим вкратце эти модели в логическом порядке.

Примерно в 1965 г. я задался целью снабдить соотношение при соответствующей моделью, в которой «центр Вселенной» отсутствовал бы как понятие. Впервые я достиг этой цели с помощью модели случайного блуждания, описываемой в главе 32. Затем, в качестве альтернативы, я разработал модель трем, сущность которой заключалась в том, что из пространства вырезалась некая совокупность взаимно независимых и размещенных случайным образом трем случайного радиуса, причем верхняя граница радиуса могла достигать верхнего порога , который мог быть конечным или бесконечным.

Поскольку обе модели были выбраны исключительно из соображений формальной простоты, меня приятно удивило наличие у них прогнозирующей ценности. Мои теоретические корреляционные функции оказались в хорошем согласии с подобранными по кривым функциями, приведенными у Пиблса (см. , с. 243-249). < Точнее, два моих приближения совпали на двухточечной корреляции, случайные блуждания дали хорошую трех- и плохую четырехточечную корреляции, а сферические тремы оказались на высоте во всех известных корреляциях.

К сожалению, примеры, генерируемые этими моделями, выглядят совершенно нереалистично. Воспользовавшись понятием, которое я разработал специально для этой цели и о котором расскажу в главе 35, можно сказать, что мои ранние модели демонстрируют неприемлемые лакунарные свойства. В случае модели трем этот недостаток можно исправить, введя более сложные формы трем. Для модели случайного блуждания я использовал менее лакунарный «субординатор».

Таким образом, изучение скоплений галактик значительно стимулировало развитие фрактальной геометрии. В настоящее же время диапазон применений фрактальной геометрии при исследовании скоплений галактик значительно расширился, выйдя далеко за рамки тех генеральных уборок и отладок, что мы предприняли в этой главе.

ОГРАНЕННЫЕ АЛМАЗЫ, ПОХОЖИЕ НА ЗВЕЗДЫ

Распределение алмазных залежей в земной коре очень напоминает распределение звезд и галактик на небесном своде. Представьте себе большую карту мира, на которой каждая алмазная копь, каждое богатое месторождение - разрабатываемое сейчас или уже заброшенное - отмечено булавкой. Рассматривая карту с достаточно большого расстояния, мы увидим, что плотность распределения булавок чрезвычайно неравномерна. Тут и там разбросано несколько отдельных булавок, однако большая часть концентрируется в немногочисленных благословенных (или проклятых) областях. Поверхность земли внутри этих областей, в свою очередь, вовсе не вымощена равномерно алмазами. Взглянув на каждую из них вблизи, мы вновь увидим, что большая часть территории остается пустой, в то время как немногочисленные рассеянные подобласти демонстрируют значительно возросшую концентрацию алмазов. Этот процесс можно продолжать на протяжении нескольких порядков величины.

Не возникает ли у вас неодолимого желания применить в этом контексте концепцию створаживания? Со своей стороны скажу, что подобная модель существует, предложил ее де Вис, а рассмотрим мы ее в главе 39 в разделе НЕЛАКУНАРНЫЕ ФРАКТАЛЫ.

В книге Фурнье к этой иллюстрации предлагается следующее пояснение: «Мультивселенная, построенная по принципу креста или восьмигранника, не является планом нашего мира, но помогает показать возможность существования бесконечного ряда подобных последовательных вселенных без возникновения эффекта «пылающего неба». Количество материи в каждой мировой сфере прямо пропорционально ее радиусу. Это условие является необходимым для соблюдения законов тяготения и излучения. В некоторых направлениях небо выглядит совершенно черным - несмотря на то, что ряд вселенных бесконечен. «Мировым числом» в данном случае является , а не , как в реальном мире». вместо . Построение продолжено на один этап дальше, чем это возможно на рис. 141.

(Динамические) фракталы

Фракталы этого типа возникают при исследовании нелинейных динамических систем (отсюда и название). Поведение такой системы можно описать комплексной нелинейной функцией (многочленом) f(z). Возьмем какую-нибудь начальную точку z0 на комплексной плоскости. Теперь рассмотрим бесконечную последовательность чисел на комплексной плоскости, каждое следующее из которых получается из предыдущего: z0, z1 = f(z0), z2 = f(z1), ... zn+1 = f(zn). В зависимости от начальной точки z0 такая последовательность может вести себя по-разному: стремиться к бесконечности при n → ∞; сходиться к какой-то конечной точке; циклически принимать ряд фиксированных значений; возможны и более сложные варианты.

Таким образом, любая точка z комплексной плоскости имеет свой характер поведения при итерациях функции f(z), а вся плоскость делится на части. При этом точки, лежащие на границах этих частей, обладают таким свойством: при сколь угодно малом смещении характер их поведения резко меняется (такие точки называют точками бифуркации). Так вот, оказывается, что множества точек, имеющих один конкретный тип поведения, а также множества бифуркационных точек часто имеют фрактальные свойства. Это и есть множества Жюлиа для функции f(z).

Множество Мандельброта строится несколько иначе. Рассмотрим функцию fc(z) = z2 + с, где c - комплексное число. Построим последовательность этой функции с z0 = 0, в зависимости от параметра с она может расходиться к бесконечности или оставаться ограниченной. При этом все значения с, при которых эта последовательность ограничена, как раз и образуют множество Мандельброта. Оно было детально изучено самим Мандельбротом и другими математиками, которые открыли немало интересных свойств этого множества.

Видно, что определения множеств Жюлиа и Мандельброта похожи друг на друга. На самом деле эти два множества тесно связаны. А именно, множество Мандельброта - это все значения комплексного параметра c, при которых множество Жюлиа fc(z) связно (множество называется связным, если его нельзя разбить на две непересекающиеся части, с некоторыми дополнительными условиями).

Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоватся терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д.

Известно, что нелинейные динамические системы обладают несолькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят - аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.

В качестве примера рассмотрим множество Мандельброта (см. pис.3 и рис.4). Алгоритм его построения достаточно прост и основан на простом итеративном выражении:

Z = Z[i] * Z[i] + C,

где Zi и C - комплексные переменные. Итерации выполняются для каждой стартовой точки C прямоугольной или квадратной области - подмножестве комплексной плоскости. Итерационный процесс продолжается до тех пор, пока Z[i] не выйдет за пределы окружности радиуса 2, центр которой лежит в точке (0,0), (это означает, что аттрактор динамической системы находится в бесконечности), или после достаточно большого числа итераций (например 200-500) Z[i] сойдется к какой-нибудь точке окружности. В зависимости от количества итераций, в течении которых Z[i] оставалась внутри окружности, можно установить цвет точки C (если Z[i] остается внутри окружности в течение достаточно большого количества итераций, итерационный процесс прекращается и эта точка растра окрашивается в черный цвет).

Вышеописанный алгоритм дает приближение к так называемому множеству Мандельброта. Множеству Мандельброта принадлежат точки, которые в течение бесконечного числа итераций не уходят в бесконечность (точки имеющие черный цвет). Точки принадлежащие границе множества (именно там возникает сложные структуры) уходят в бесконечность за конечное число итераций, а точки лежащие за пределами множества, уходят в бесконечность через несколько итераций (белый фон).

Примеры алгебраических фракталов:

• Множество Мандельброта
• Множества Жюлиа
• Фрактал Галлея
• Фрактал Ньютона